Refine listing
Actions for selected content:
411 results in 35Jxx
THE
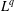 $L^{q}$ ESTIMATES OF RIESZ TRANSFORMS ASSOCIATED TO SCHRÖDINGER OPERATORS
$L^{q}$ ESTIMATES OF RIESZ TRANSFORMS ASSOCIATED TO SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 25 April 2016, pp. 290-309
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Compact embedding results of Sobolev spaces and positive solutions to an elliptic equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 11 April 2016, pp. 693-721
- Print publication:
- August 2016
-
- Article
- Export citation
A fourth-order seven-point cubature on regular hexagons
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 175-185
-
- Article
-
- You have access
- Export citation
Concentration of solutions of equations of nonlinear Schrödinger type with vector potential: infinite-bump solutions and non-degeneracy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 625-646
- Print publication:
- June 2016
-
- Article
- Export citation
ON THE FIRST EIGENCONE FOR THE FINSLER LAPLACIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 316-325
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Existence and multiplicity of solutions for an indefinite Kirchhoff-type equation in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 435-448
- Print publication:
- April 2016
-
- Article
- Export citation
Development of a Combined Compact Difference Scheme to Simulate Soliton Collision in a Shallow Water Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 603-631
- Print publication:
- March 2016
-
- Article
- Export citation
THE MEAN CURVATURE EQUATION ON SEMIDIRECT PRODUCTS
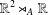 $\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$: HEIGHT ESTIMATES AND SCHERK-LIKE GRAPHS
$\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$: HEIGHT ESTIMATES AND SCHERK-LIKE GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 118-144
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Solutions for a Kirchhoff Equation with Weight and Nonlinearity with Subcritical and Critical Caffarelli–Kohn–Nirenberg Growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 925-944
-
- Article
- Export citation
The regularity and stability of solutions to semilinear fourth-order elliptic problems with negative exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 07 January 2016, pp. 195-212
- Print publication:
- February 2016
-
- Article
- Export citation
SPECTRAL THEORETIC CHARACTERIZATION OF THE MASSLESS DIRAC ACTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 08 March 2016, pp. 701-718
- Print publication:
- 2016
-
- Article
-
- You have access
- Open access
- Export citation
Solutions of p-Laplace Equations with Infinite Boundary Values: The case of Non-Autonomous and Non-Monotone Nonlinearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 959-987
-
- Article
- Export citation
Qualitative Analysis of Solutions for a Class of Anisotropic Elliptic Equations with Variable Exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 15 December 2015, pp. 541-557
-
- Article
- Export citation
New Conditions for the Existence of Infinitely Many Solutions for a Quasi-Linear Problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 15 December 2015, pp. 655-669
-
- Article
- Export citation
On a singular semilinear elliptic problem with an asymptotically linear nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 11 December 2015, pp. 59-77
- Print publication:
- February 2016
-
- Article
- Export citation
Remarks on Entire Solutions for Two Fourth-Order Elliptic Problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 23 November 2015, pp. 777-786
-
- Article
- Export citation
High Order Finite Difference Discretization for Composite Grid Hierarchy and Its Applications
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1211-1233
- Print publication:
- November 2015
-
- Article
- Export citation
WEAK POTENTIAL CONDITIONS FOR SCHRÖDINGER EQUATIONS WITH CRITICAL NONLINEARITIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 272-288
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Gradient estimates for semilinear elliptic systems and other related results
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 22 October 2015, pp. 1313-1330
- Print publication:
- December 2015
-
- Article
- Export citation
Clustering layers for the Fife—Greenlee problem in ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 October 2015, pp. 107-139
- Print publication:
- February 2016
-
- Article
- Export citation
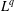
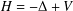
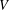
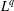
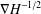
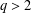
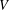
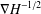
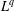
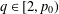
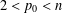
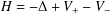
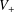
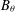
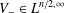
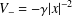

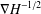
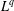
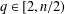
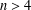
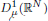 of the commonly used Sobolev space
of the commonly used Sobolev space 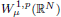 to
to 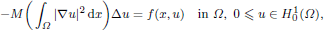
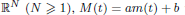 and
and 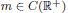 . We require that
. We require that 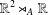
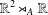
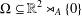
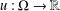

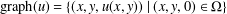

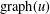
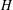

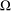
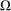
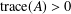

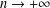
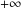
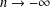


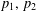
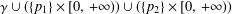
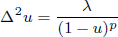
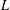

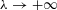

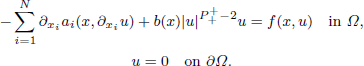
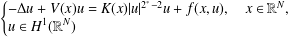
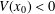
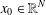
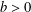
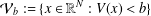
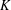
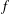
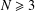
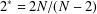
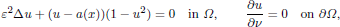
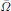 . Let
. Let 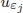 with
with 