Refine listing
Actions for selected content:
411 results in 35Jxx
Infinitely many non-radial singular solutions of
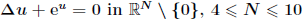
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 133-147
- Print publication:
- February 2018
-
- Article
- Export citation
Infinitely many solutions for three classes of self-similar equations with p-Laplace operator: Gelfand, Joseph–Lundgren and MEMS problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 341-356
- Print publication:
- April 2018
-
- Article
- Export citation
A multi-species chemotaxis system: Lyapunov functionals, duality, critical mass
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 515-542
-
- Article
- Export citation
Infinitely many solutions for equations of p(x)-Laplace type with the nonlinear Neumann boundary condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 August 2017, pp. 1-31
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Morse index and symmetry breaking for an elliptic equation with negative exponent in expanding annuli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1215-1232
- Print publication:
- December 2017
-
- Article
- Export citation
HARDY SPACES ON METRIC MEASURE SPACES WITH GENERALIZED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 162-194
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Positive solutions of Kirchhoff-type non-local elliptic equation: a bifurcation approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 875-894
- Print publication:
- August 2017
-
- Article
- Export citation
Stability analysis for positive solutions for classes of semilinear elliptic boundary-value problems with nonlinear boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 1019-1040
- Print publication:
- October 2017
-
- Article
- Export citation
On isotropic cloaking and interior transmission eigenvalue problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 22 May 2017, pp. 253-280
-
- Article
- Export citation
Bifurcation from infinity for reaction–diffusion equations under nonlinear boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 649-671
- Print publication:
- June 2017
-
- Article
- Export citation
Size estimates of unknown boundaries with a Robin-type condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 727-741
- Print publication:
- August 2017
-
- Article
- Export citation
Lotka–Volterra models with fractional diffusion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 505-528
- Print publication:
- June 2017
-
- Article
- Export citation
MULTIPLE SOLUTIONS FOR A KIRCHHOFF EQUATION WITH NONLINEARITY HAVING ARBITRARY GROWTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 98-109
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
PERTURBATIONS FROM INDEFINITE SYMMETRIC ELLIPTIC BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 February 2017, pp. 635-648
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Nonconforming Finite Element Methods for Wave Propagation in Metamaterials
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 145-166
- Print publication:
- February 2017
-
- Article
- Export citation
Infinitely Many Solutions for Schrödinger–Kirchhoff-Type Fourth-Order Elliptic Equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 1003-1020
-
- Article
- Export citation
A short remark regarding Pohozaev-type results on general domains assuming finite Morse index
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 293-297
- Print publication:
- April 2017
-
- Article
- Export citation
Infinitely many non-radial solutions for the polyharmonic Hénon equation with a critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 371-396
- Print publication:
- April 2017
-
- Article
- Export citation
On the Hardy–Sobolev equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 299-336
- Print publication:
- April 2017
-
- Article
- Export citation
Neumann to Steklov eigenvalues: asymptotic and monotonicity results
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 429-447
- Print publication:
- April 2017
-
- Article
- Export citation
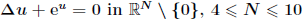


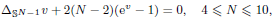
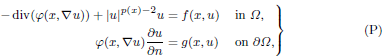
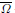
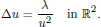
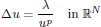
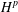
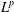
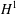
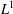
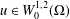








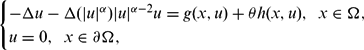

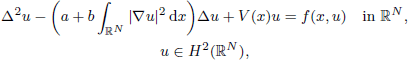
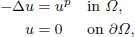
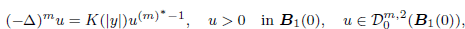
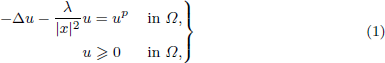
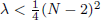 . Using a suitable map we transform problem (1) into another one without the singularity 1/|
. Using a suitable map we transform problem (1) into another one without the singularity 1/|