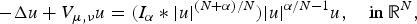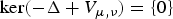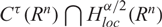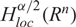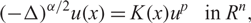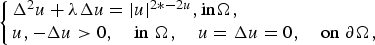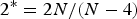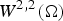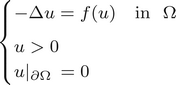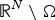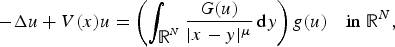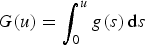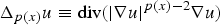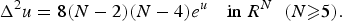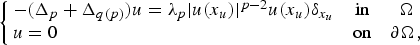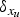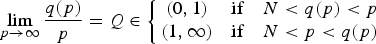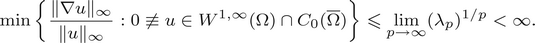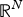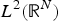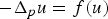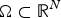Refine listing
Actions for selected content:
411 results in 35Jxx
Liouville-type theorems and existence results for stable solutions to weighted Lane–Emden equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1567-1579
- Print publication:
- June 2020
-
- Article
- Export citation
Groundstates for Choquard type equations with Hardy–Littlewood–Sobolev lower critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1377-1400
- Print publication:
- June 2020
-
- Article
- Export citation
Monotonicity of non-Liouville property for positive solutions of skew product elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1429-1449
- Print publication:
- June 2020
-
- Article
- Export citation
ON NONLOCAL NONLINEAR ELLIPTIC PROBLEMS WITH THE FRACTIONAL LAPLACIAN
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 75-84
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Existence and multiplicity of positive solutions for a fourth-order elliptic equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 28 January 2019, pp. 1053-1069
- Print publication:
- April 2020
-
- Article
- Export citation
A note on a positive solution of a null mass nonlinear field equation in exterior domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 841-870
- Print publication:
- April 2020
-
- Article
- Export citation
Spectral transitions for Aharonov-Bohm Laplacians on conical layers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1663-1687
- Print publication:
- December 2019
-
- Article
- Export citation
Existence of solutions for critical Choquard equations via the concentration-compactness method
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 921-954
- Print publication:
- April 2020
-
- Article
- Export citation
A p(x)-Laplacian extension of the Díaz-Saa inequality and some applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 205-232
- Print publication:
- February 2020
-
- Article
- Export citation
Radial symmetry of non-maximal entire solutions of a bi-harmonic equation with exponential nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1603-1625
- Print publication:
- December 2019
-
- Article
- Export citation
A priori bounds and multiplicity of positive solutions for p-Laplacian Neumann problems with sub-critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 73-102
- Print publication:
- February 2020
-
- Article
- Export citation
A CLASS OF CRITICAL KIRCHHOFF PROBLEM ON THE HYPERBOLIC SPACE
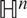 $\mathbb{H}^{{\it n}}$
$\mathbb{H}^{{\it n}}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 January 2019, pp. 109-122
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
On critical exponents of a k-Hessian equation in the whole space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1555-1575
- Print publication:
- December 2019
-
- Article
- Export citation
Asymptotic behaviour as p → ∞ of least energy solutions of a (p, q(p))-Laplacian problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1493-1522
- Print publication:
- December 2019
-
- Article
- Export citation
Infinite multiplicity of stable entire solutions for a semilinear elliptic equation with exponential nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1371-1404
- Print publication:
- October 2019
-
- Article
- Export citation
On the classification of standing wave solutions to a coupled Schrödinger system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1347-1370
- Print publication:
- October 2019
-
- Article
- Export citation
Some generic properties of Schrödinger operators with radial potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1435-1451
- Print publication:
- December 2019
-
- Article
- Export citation
On a property of the nodal set of least energy sign-changing solutions for quasilinear elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1163-1173
- Print publication:
- October 2019
-
- Article
- Export citation
On the boundary regularity of phase-fields for Willmore's energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1017-1035
- Print publication:
- August 2019
-
- Article
- Export citation
Bifurcation and standing wave solutions for a quasilinear Schrödinger equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 939-968
- Print publication:
- August 2019
-
- Article
- Export citation