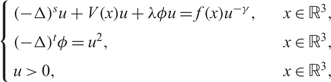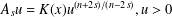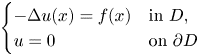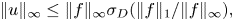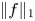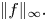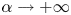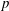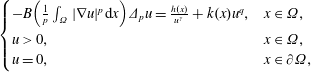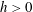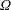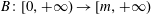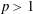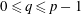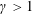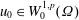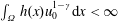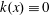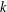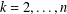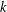Refine listing
Actions for selected content:
411 results in 35Jxx
A novel Landau-de Gennes model with quartic elastic terms
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 March 2020, pp. 177-198
-
- Article
- Export citation
FRACTIONAL SCHRÖDINGER–POISSON SYSTEM WITH SINGULARITY: EXISTENCE, UNIQUENESS, AND ASYMPTOTIC BEHAVIOR
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 179-192
- Print publication:
- January 2021
-
- Article
- Export citation
On approximating minimizers of convex functionals with a convexity constraint by singular Abreu equations without uniform convexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 356-376
- Print publication:
- February 2021
-
- Article
- Export citation
PERTURBATION THEOREMS FOR FRACTIONAL CRITICAL EQUATIONS ON BOUNDED DOMAINS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 159-178
- Print publication:
- October 2021
-
- Article
- Export citation
Multiple bound states of higher topological type for semi-classical Choquard equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 329-355
- Print publication:
- February 2021
-
- Article
- Export citation
On supercritical problems involving the Laplace operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 27 February 2020, pp. 187-201
- Print publication:
- February 2021
-
- Article
- Export citation
DISTINCT SOLUTIONS TO GENERATED JACOBIAN EQUATIONS CANNOT INTERSECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 462-470
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Nondegeneracy of the bubble for the critical p-Laplace equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 151-168
- Print publication:
- February 2021
-
- Article
- Export citation
Radial symmetry of minimizers to the weighted Dirichlet energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 169-186
- Print publication:
- February 2021
-
- Article
- Export citation
On the L∞-maximization of the solution of Poisson's equation: Brezis–Gallouet–Wainger type inequalities and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 79-92
- Print publication:
- February 2021
-
- Article
- Export citation
Nonlinear fractional Laplacian problems with nonlocal ‘gradient terms’
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 2682-2718
- Print publication:
- October 2020
-
- Article
- Export citation
LYAPUNOV-TYPE INEQUALITY FOR EXTREMAL PUCCI’S EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 29 January 2020, pp. 416-430
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Regularity for solutions of fully nonlinear elliptic equations with nonhomogeneous degeneracy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 29 January 2020, pp. 110-132
- Print publication:
- February 2021
-
- Article
- Export citation
Existence, non-existence and blow-up behaviour of minimizers for the mass-critical fractional non-linear Schrödinger equations with periodic potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 3252-3292
- Print publication:
- December 2020
-
- Article
- Export citation
Many synchronized vector solutions for a Bose–Einstein system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 3293-3320
- Print publication:
- December 2020
-
- Article
- Export citation
Generalized eigenvalues of the (P, 2)-Laplacian under a parametric boundary condition
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 287-303
-
- Article
- Export citation
Existence and Uniqueness of Solutions to Singular p-Laplace Equations of Kirchhoff Type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 677-691
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Gradient estimates for the constant mean curvature equation in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 09 December 2019, pp. 3216-3230
- Print publication:
- December 2020
-
- Article
- Export citation
On supercritical nonlinear Schrödinger equations with ellipse-shaped potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 02 December 2019, pp. 3187-3215
- Print publication:
- December 2020
-
- Article
- Export citation
THE DISTRIBUTIONAL
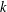 $k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES
$k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 23 October 2019, pp. 496-507
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation