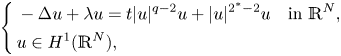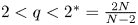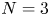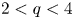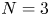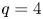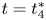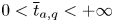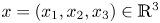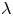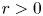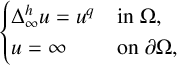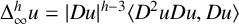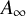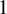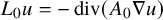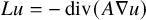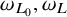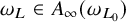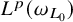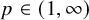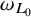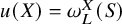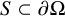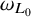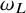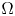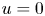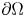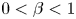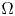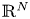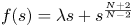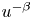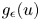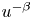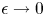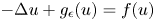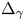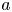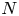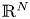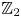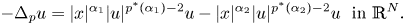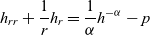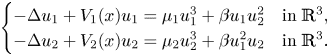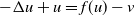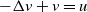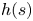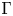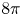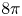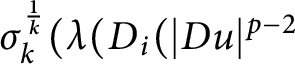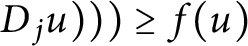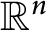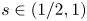Refine listing
Actions for selected content:
411 results in 35Jxx
On some nonlinear Schrödinger equations in ℝN
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1503-1528
- Print publication:
- October 2023
-
- Article
- Export citation
BOUNDARY BLOW-UP SOLUTIONS TO EQUATIONS INVOLVING THE INFINITY LAPLACIAN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 337-358
- Print publication:
- June 2023
-
- Article
- Export citation
On the
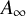 $A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
$A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 05 August 2022, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singular elliptic equations with nonlinearities of subcritical and critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 27 July 2022, pp. 652-690
-
- Article
- Export citation
A Berestycki–Lions type result for a class of degenerate elliptic problems involving the Grushin operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 July 2022, pp. 1244-1271
- Print publication:
- August 2023
-
- Article
- Export citation
On a class of critical N-Laplacian problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 27 June 2022, pp. 556-576
-
- Article
- Export citation
The ground states of quasilinear Hénon equation with double weighted critical exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 03 June 2022, pp. 1037-1044
- Print publication:
- June 2023
-
- Article
- Export citation
Steady states of thin-film equations with van der Waals force with mass constraint
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 280-302
-
- Article
- Export citation
Steady state diffusion in tubular structures: Assessment of one-dimensional models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 262-279
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-degeneracy of synchronized vector solutions for weakly coupled nonlinear schrödiner systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 22 April 2022, pp. 441-459
-
- Article
- Export citation
Existence of solution for a class of activator–inhibitor systems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 April 2022, pp. 98-113
- Print publication:
- January 2023
-
- Article
- Export citation
Inhomogeneous Helmholtz equations in wave guides – existence and uniqueness results with energy methods
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 211-237
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locations of interior transition layers to inhomogeneous transition problems in higher -dimensional domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 08 March 2022, pp. 764-783
- Print publication:
- June 2023
-
- Article
- Export citation
Measure data elliptic problems with generalized Orlicz growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 March 2022, pp. 588-618
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Soliton solutions for a class of Schrödinger equations with a positive quasilinear term and critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 279-301
-
- Article
- Export citation
Γ-convergence and stochastic homogenization of degenerate integral functionals in weighted Sobolev spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 February 2022, pp. 491-544
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stationary solutions to the Keller–Segel equation on curved planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 327-343
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bifurcation of elastic curves with modulated stiffness
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 January 2022, pp. 28-54
-
- Article
-
- You have access
- HTML
- Export citation
Necessary and sufficient conditions on global solvability for the p-k-Hessian inequalities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 1004-1019
- Print publication:
- December 2022
-
- Article
- Export citation
Periodic solutions for one-dimensional nonlinear nonlocal problem with drift including singular nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 December 2021, pp. 229-261
- Print publication:
- February 2023
-
- Article
- Export citation