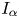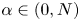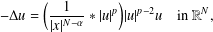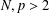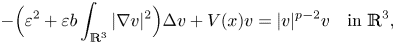Refine listing
Actions for selected content:
411 results in 35Jxx
ASYMPTOTIC ANALYSIS FOR THE MEAN FIRST PASSAGE TIME IN FINITE OR SPATIALLY PERIODIC 2D DOMAINS WITH A CLUSTER OF SMALL TRAPS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 1-22
-
- Article
- Export citation
Existence of solution for elliptic equations with supercritical Trudinger–Moser growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 291-310
- Print publication:
- April 2022
-
- Article
- Export citation
Fast and slow decay solutions for supercritical fractional elliptic problems in exterior domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 28-53
- Print publication:
- February 2022
-
- Article
- Export citation
SCHRÖDINGER OPERATORS AND THE KATO SQUARE ROOT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 162-163
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
A characterization of singular Schrödinger operators on the half-line
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 923-941
- Print publication:
- December 2021
-
- Article
- Export citation
Borderline gradient estimates at the boundary in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 1920-1953
- Print publication:
- December 2021
-
- Article
- Export citation
Prescribed k-symmetric curvature hypersurfaces in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 26 November 2020, pp. 886-901
- Print publication:
- December 2021
-
- Article
- Export citation
Comparing the best-reply strategy and mean-field games: The stationary case
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 79-110
-
- Article
- Export citation
The Fourier extension operator of distributions in Sobolev spaces of the sphere and the Helmholtz equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 16 November 2020, pp. 1768-1789
- Print publication:
- December 2021
-
- Article
- Export citation
Large number of bubble solutions for a fractional elliptic equation with almost critical exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 1642-1681
- Print publication:
- October 2021
-
- Article
- Export citation
Bloch wave homogenisation of quasiperiodic media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 58-78
-
- Article
- Export citation
Optimal global asymptotic behaviour of the solution to a class of singular Dirichlet problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 1116-1134
- Print publication:
- June 2021
-
- Article
- Export citation
ESTIMATES AND RIGIDITY FOR STABLE SOLUTIONS TO SOME NONLINEAR ELLIPTIC PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 10 September 2020, pp. 335-337
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
Bounded solutions for an ordinary differential system from the Ginzburg–Landau theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 14 August 2020, pp. 3378-3408
- Print publication:
- December 2020
-
- Article
- Export citation
Some further results on the nonlocal p-Laplacian type problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 07 August 2020, pp. 953-970
- Print publication:
- June 2021
-
- Article
- Export citation
Quasilinear elliptic inequalities with Hardy potential and nonlocal terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 July 2020, pp. 1075-1093
- Print publication:
- June 2021
-
- Article
- Export citation
STABLE SOLUTIONS TO THE STATIC CHOQUARD EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 471-478
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Estimates for sums and gaps of eigenvalues of Laplacians on measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 842-861
- Print publication:
- April 2021
-
- Article
- Export citation
Semi-classical solutions for Kirchhoff type problem with a critical frequency
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 May 2020, pp. 761-798
- Print publication:
- April 2021
-
- Article
- Export citation
The spectrum of the mean curvature operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 April 2020, pp. 451-463
- Print publication:
- April 2021
-
- Article
- Export citation