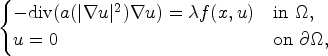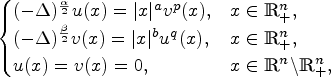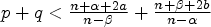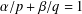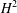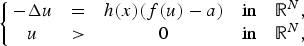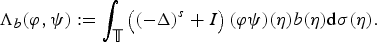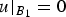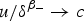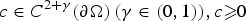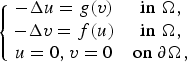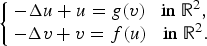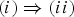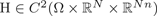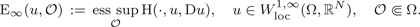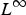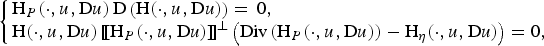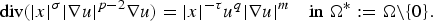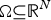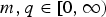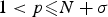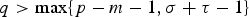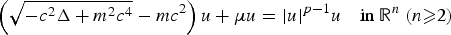Refine listing
Actions for selected content:
411 results in 35Jxx
Existence of solution for quasilinear equations involving local conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3074-3086
- Print publication:
- December 2020
-
- Article
- Export citation
Liouville theorem for fractional Hénon–Lane–Emden systems on a half space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3060-3073
- Print publication:
- December 2020
-
- Article
- Export citation
EXISTENCE AND UNIQUENESS OF WEAK AND CLASSICAL SOLUTIONS FOR A FOURTH-ORDER SEMILINEAR BOUNDARY VALUE PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 3 / July 2019
- Published online by Cambridge University Press:
- 19 August 2019, pp. 305-319
-
- Article
-
- You have access
- Export citation
POSITIVE GROUND STATES FOR A CLASS OF SUPERLINEAR
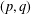 $(p,q)$-LAPLACIAN COUPLED SYSTEMS INVOLVING SCHRÖDINGER EQUATIONS
$(p,q)$-LAPLACIAN COUPLED SYSTEMS INVOLVING SCHRÖDINGER EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 193-216
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
NEW GLOBAL LOGARITHMIC STABILITY RESULTS ON THE CAUCHY PROBLEM FOR ELLIPTIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 141-145
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Effective multi-scale approach to the Schrödinger cocycle over a skew-shift base
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 17 April 2019, pp. 2788-2853
- Print publication:
- October 2020
-
- Article
- Export citation
Existence of positive solutions for a class of semipositone problem in whole ℝN
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 05 April 2019, pp. 2349-2367
- Print publication:
- October 2020
-
- Article
- Export citation
Asymptotic Behaviour of the Energy Integral of a Two-Parameter Homogenization Problem with Nonlinear Periodic Robin Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 22 March 2019, pp. 985-1016
-
- Article
- Export citation
Bilinear forms on potential spaces in the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 19 March 2019, pp. 2117-2154
- Print publication:
- August 2020
-
- Article
- Export citation
Sharp estimates of semistable radial solutions of k-Hessian equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 March 2019, pp. 2083-2115
- Print publication:
- August 2020
-
- Article
- Export citation
Standing waves of modified Schrödinger equations coupled with the Chern–Simons gauge theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1915-1936
- Print publication:
- August 2020
-
- Article
- Export citation
Positive solutions of semilinear elliptic problems with a Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 February 2019, pp. 1791-1804
- Print publication:
- August 2020
-
- Article
- Export citation
Ground state solutions of Hamiltonian elliptic systems in dimension two
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 February 2019, pp. 1737-1768
- Print publication:
- August 2020
-
- Article
- Export citation
Corrigendum to: Dirichlet and Neumann boundary conditions for the p-Laplace operator: What is in between?
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1689-1691
- Print publication:
- December 2019
-
- Article
- Export citation
A pointwise characterisation of the PDE system of vectorial calculus of variations in L∞
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1653-1669
- Print publication:
- August 2020
-
- Article
- Export citation
Decay rates at infinity for solutions to periodic Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1113-1126
- Print publication:
- June 2020
-
- Article
- Export citation
Gradient estimates for nonlinear elliptic equations with a gradient-dependent nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1361-1376
- Print publication:
- June 2020
-
- Article
- Export citation
On critical and supercritical pseudo-relativistic nonlinear Schrödinger equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1241-1263
- Print publication:
- June 2020
-
- Article
- Export citation
Dual ground state solutions for the critical nonlinear Helmholtz equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1155-1186
- Print publication:
- June 2020
-
- Article
- Export citation
Non-Zero Radial Solutions for Elliptic Systems with Coupled Functional BCs in Exterior Domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 747-769
-
- Article
- Export citation