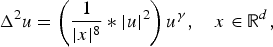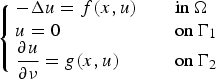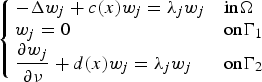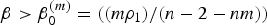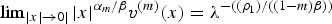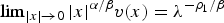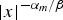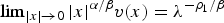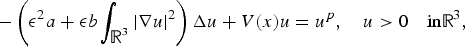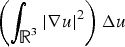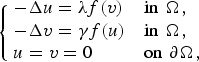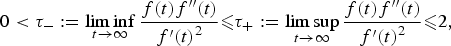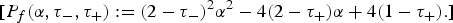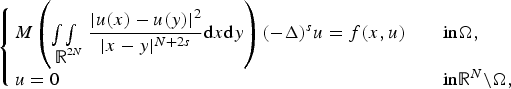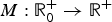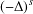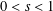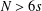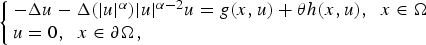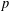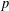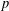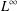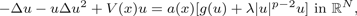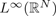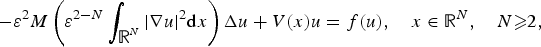Refine listing
Actions for selected content:
411 results in 35Jxx
Classification of nonnegative solutions to a bi-harmonic equation with Hartree type nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 979-994
- Print publication:
- August 2019
-
- Article
- Export citation
Morse index and symmetry for elliptic problems with nonlinear mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 305-324
- Print publication:
- April 2019
-
- Article
- Export citation
Singular limits and properties of solutions of some degenerate elliptic and parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 353-385
- Print publication:
- April 2019
-
- Article
- Export citation
Nonlocal problems arising from the birth-jump processes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 447-469
- Print publication:
- April 2019
-
- Article
- Export citation
A quantitative Carleman estimate for second-order elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 915-938
- Print publication:
- August 2019
-
- Article
- Export citation
Existence of normalized solutions for nonlinear fractional Schrödinger equations with trapping potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 617-653
- Print publication:
- June 2019
-
- Article
- Export citation
Multi-peak positive solutions to a class of Kirchhoff equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1097-1122
- Print publication:
- August 2019
-
- Article
- Export citation
Regularity of the extremal solutions associated with elliptic systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1037-1046
- Print publication:
- August 2019
-
- Article
- Export citation
Existence results for Kirchhoff–type superlinear problems involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1061-1081
- Print publication:
- August 2019
-
- Article
- Export citation
A mean field equation involving positively supported probability measures: blow-up phenomena and variational aspects
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 325-352
- Print publication:
- April 2019
-
- Article
- Export citation
AN IMPROVED RESULT ON GROUND STATE SOLUTIONS OF QUASILINEAR SCHRÖDINGER EQUATIONS WITH SUPER-LINEAR NONLINEARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 231-241
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
INFINITELY MANY SOLUTIONS FOR NONLOCAL SYSTEMS INVOLVING FRACTIONAL LAPLACIAN UNDER NONCOMPACT SETTINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 215-233
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Multiple Solutions of Sublinear Quasilinear Schrödinger Equations with Small Perturbations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 471-488
-
- Article
- Export citation
THE UNIQUE CONTINUATION PROPERTY OF
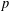 $p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
$p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 219-230
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
RECOVERY OF NON-COMPACTLY SUPPORTED COEFFICIENTS OF ELLIPTIC EQUATIONS ON AN INFINITE WAVEGUIDE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1573-1600
- Print publication:
- September 2020
-
- Article
- Export citation
On the avascular ellipsoidal tumour growth model within a nutritive environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 111-142
-
- Article
- Export citation
Three Solutions for a Singular Quasilinear Elliptic Problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 179-196
-
- Article
- Export citation
TWO-SIDED ESTIMATES FOR POSITIVE SOLUTIONS OF SUPERLINEARELLIPTIC BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 465-473
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Least Energy Nodal Solutions for a Defocusing Schrödinger Equation with Supercritical Exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 August 2018, pp. 1-23
-
- Article
- Export citation
Existence and Concentration of Positive Solutions for Nonlinear Kirchhoff-Type Problems with a General Critical Nonlinearity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 17 July 2018, pp. 1023-1040
-
- Article
- Export citation