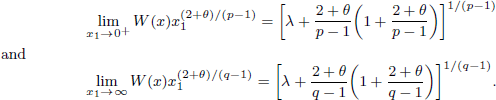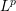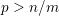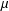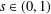Refine listing
Actions for selected content:
411 results in 35Jxx
Existence results for semilinear problems in the two-dimensional hyperbolic space involving critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 141-176
- Print publication:
- February 2017
-
- Article
- Export citation
MINIMIZING DIRICHLET EIGENVALUES ON CUBOIDS OF UNIT MEASURE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 469-482
- Print publication:
- 2017
-
- Article
- Export citation
Theorems of the Phragmén–Lindelöf Type for Subfunctions in a Cone
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 29 December 2016, pp. 739-751
-
- Article
- Export citation
EXISTENCE OF POSITIVE SOLUTION FOR INDEFINITE KIRCHHOFF EQUATION IN EXTERIOR DOMAINS WITH SUBCRITICAL OR CRITICAL GROWTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 329-340
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
A Static Condensation Reduced Basis Element Approach for the Reynolds Lubrication Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 126-148
- Print publication:
- January 2017
-
- Article
- Export citation
Optimal Hardy inequalities in cones
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 89-124
- Print publication:
- February 2017
-
- Article
- Export citation
Dirichlet problems for fully anisotropic elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 25-60
- Print publication:
- February 2017
-
- Article
- Export citation
Multiple solutions for a critical fractional elliptic system involving concave–convex nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 27 October 2016, pp. 1167-1193
- Print publication:
- December 2016
-
- Article
- Export citation
Multiplicity of Multi-Bump Type Nodal Solutions for A Class of Elliptic Problems with Exponential Critical Growth in ℝ2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 273-297
-
- Article
- Export citation
Asymptotic behaviour and symmetry of positive solutions to nonlinear elliptic equations in a half-space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1243-1263
- Print publication:
- December 2016
-
- Article
- Export citation
THE MODIFIED QUANTUM WIGNER SYSTEM IN WEIGHTED
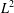 $L^{2}$ -SPACE
$L^{2}$ -SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 73-83
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Weak solutions of complex Hessian equations on compact Hermitian manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 09 September 2016, pp. 2221-2248
- Print publication:
- November 2016
-
- Article
- Export citation
EXISTENCE OF A WEAK SOLUTION FOR A CLASS OF FRACTIONAL LAPLACIAN EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 392-404
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A Simple Method for Computing Singular or Nearly Singular Integrals on Closed Surfaces
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 733-753
- Print publication:
- September 2016
-
- Article
- Export citation
DIRECT EXPRESSION OF INCOMPATIBILITY IN CURVILINEAR SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 33-50
-
- Article
-
- You have access
- Export citation
Nodal vector solutions with clustered peaks for nonlinear elliptic equations in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 947-982
- Print publication:
- October 2016
-
- Article
- Export citation
Unified a Priori Error Estimate and a Posteriori Error Estimate of CIP-FEM for Elliptic Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 517-535
- Print publication:
- August 2016
-
- Article
- Export citation
On a Class of Semilinear Elliptic Eigenvalue Problems in ℝ2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 107-126
-
- Article
- Export citation
Existence of positive solutions for a semipositone p-Laplacian problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 475-482
- Print publication:
- June 2016
-
- Article
- Export citation
Parameter-Free Time Adaptivity Based on Energy Evolution for the Cahn-Hilliard Equation
- Part of
- Partial differential equations, boundary value problems
- Equations of mathematical physics and other areas of application
- Partial differential equations, initial value and time-dependent initial-boundary value problems
- Miscellaneous topics - Partial differential equations
- Elliptic equations and systems
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1542-1563
- Print publication:
- May 2016
-
- Article
- Export citation
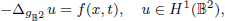
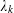
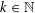
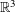
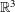
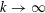
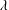
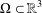
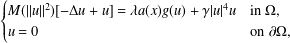
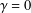
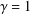
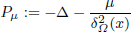
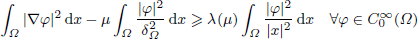
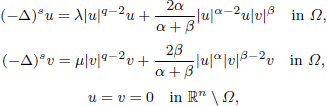
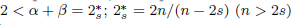 is the fractional critical Sobolev exponent.
is the fractional critical Sobolev exponent.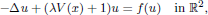
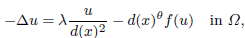
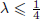 ,
,