Refine listing
Actions for selected content:
411 results in 35Jxx
CONTACT PROBLEMS FOR NONLINEARLY ELASTIC MATERIALS: WEAK SOLVABILITY INVOLVING DUAL LAGRANGE MULTIPLIERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 03 August 2011, pp. 160-178
-
- Article
-
- You have access
- Export citation
A biharmonic equation with singular nonlinearity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 14 June 2011, pp. 155-166
-
- Article
-
- You have access
- Export citation
FLOWS AND INVARIANCE FOR DEGENERATE ELLIPTIC OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 317-339
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
HÖLDER ESTIMATES FOR LINEAR SECOND-ORDER EQUATIONS: CORRIGENDUM
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 18 May 2011, p. 328
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
ON AN ANTIPLANE CRACK PROBLEM FOR FUNCTIONALLY GRADED ELASTIC MATERIALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 1 / July 2010
- Published online by Cambridge University Press:
- 21 April 2011, pp. 69-86
-
- Article
-
- You have access
- Export citation
REGULARITY OF MONGE–AMPÈRE EQUATIONS IN OPTIMAL TRANSPORTATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 27 January 2011, pp. 173-176
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Solvability conditions for some non-Fredholm operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 30 November 2010, pp. 249-271
-
- Article
-
- You have access
- Export citation
HÖLDER ESTIMATES FOR LINEAR SECOND-ORDER EQUATIONS
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 315-327
- Print publication:
- July 2011
-
- Article
- Export citation
Solutions of perturbed Schrödinger equations with electromagnetic fields and critical nonlinearity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 131-147
-
- Article
-
- You have access
- Export citation
ENTROPY AND RENORMALIZED SOLUTIONS FOR THE p(x)-LAPLACIAN EQUATION WITH MEASURE DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 August 2010, pp. 459-479
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
MULTIPLE SOLUTIONS FOR RESONANT ELLIPTIC SYSTEMS VIA REDUCTION METHOD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 April 2010, pp. 211-220
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Solutions for Semilinear Elliptic Systems with Critical Sobolev Exponent and Hardy Potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-33
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Superlinear elliptic equation for fully nonlinear operators without growth restrictions for the data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 125-141
-
- Article
-
- You have access
- Export citation
Quasilinear elliptic problems with critical exponents and Hardy terms in ℝN
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 175-193
-
- Article
-
- You have access
- Export citation
BOUNDARY BEHAVIOR OF SUPERHARMONIC FUNCTIONS SATISFYING NONLINEAR INEQUALITIES IN A PLANAR SMOOTH DOMAIN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 253-261
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Three non-trivial solutions for not necessarily coercive p-Laplacian equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 679-688
-
- Article
-
- You have access
- Export citation
Positive solutions of a nonlinear Sturm–Liouville boundary-value problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 561-568
-
- Article
-
- You have access
- Export citation
SIGN-CHANGING SOLUTIONS FOR A CLASS OF NONLINEAR SCHRÖDINGER EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 294-305
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Multiplicity theorems for semilinear elliptic problems depending on a parameter
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 171-180
-
- Article
-
- You have access
- Export citation
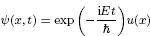
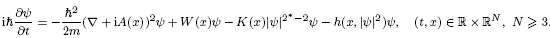
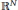
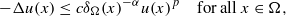
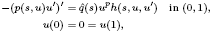
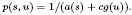
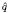 to be non-negative, continuous functions,
to be non-negative, continuous functions, 