Refine listing
Actions for selected content:
304 results in 60Cxx
The censored Markov chain and the best augmentation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 623-629
- Print publication:
- September 1996
-
- Article
- Export citation
Simple random walk statistics. Part I: Discrete time results
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 311-330
- Print publication:
- September 1996
-
- Article
- Export citation
Simple random walk statistics. Part II: Continuous time results
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 331-339
- Print publication:
- September 1996
-
- Article
- Export citation
On the distribution of distances in recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 749-757
- Print publication:
- September 1996
-
- Article
- Export citation
Potentially unlimited variance reduction in importance sampling of Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 166-188
- Print publication:
- March 1996
-
- Article
- Export citation
Recursive relations for the distribution of waiting times in a Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 48-56
- Print publication:
- March 1996
-
- Article
- Export citation
Compound Poisson approximations for word patterns under Markovian hypotheses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 877-892
- Print publication:
- December 1995
-
- Article
- Export citation
Probability bounds on the finite sum of the binary sequence of order k
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1014-1027
- Print publication:
- December 1995
-
- Article
- Export citation
On crossing times for multidimensional walks with skip-free components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 991-1006
- Print publication:
- December 1995
-
- Article
- Export citation
Measure generation by Euler functionals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 606-626
- Print publication:
- September 1995
-
- Article
- Export citation
Random high-dimensional orders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 161-184
- Print publication:
- March 1995
-
- Article
- Export citation
Dixie cups: sampling with replacement from a finite population
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 940-948
- Print publication:
- December 1994
-
- Article
- Export citation
Another Look at the Ehrenfest Urn Via Electric Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 820-824
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
Uniqueness of maximum values in discrete distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 757-764
- Print publication:
- September 1994
-
- Article
- Export citation
Generalized Bonferroni inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 409-417
- Print publication:
- June 1994
-
- Article
- Export citation
Some joint distributions in Bernoulli excursions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 239-250
- Print publication:
- 1994
-
- Article
- Export citation
Further studies of bivariate Bonferroni-type inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 63-69
- Print publication:
- 1994
-
- Article
- Export citation
Compound poisson approximations for the numbers of extreme spacings
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 847-874
- Print publication:
- December 1993
-
- Article
- Export citation
Fluctuation theory for the Ehrenfest urn via electric networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 472-476
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Improved Poisson approximations for word patterns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 334-347
- Print publication:
- June 1993
-
- Article
- Export citation
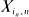 is asymptotically normal in several settings.
is asymptotically normal in several settings.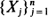 with state space consisting of the
with state space consisting of the 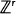 (or
(or 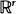 ), one of whose components is skip-free. We obtain identities for distributions of hitting times for the components of the process generalizing the well-known one for the one-dimensional case. These relations reflect the fact that in this case spatial and time coordinates play, in some sense, symmetric roles. They turn out to be useful for solving several problems. For example, they allow us to find the distribution of the number of jumps of the process, which fall in a fixed set before the skip-free component of the process hits a fixed level. Examples are given showing how our results can be applied to models in branching processes, queueing, and risk theory.
), one of whose components is skip-free. We obtain identities for distributions of hitting times for the components of the process generalizing the well-known one for the one-dimensional case. These relations reflect the fact that in this case spatial and time coordinates play, in some sense, symmetric roles. They turn out to be useful for solving several problems. For example, they allow us to find the distribution of the number of jumps of the process, which fall in a fixed set before the skip-free component of the process hits a fixed level. Examples are given showing how our results can be applied to models in branching processes, queueing, and risk theory.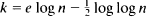 is a threshold function for the appearance of an element of degree
is a threshold function for the appearance of an element of degree 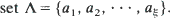 . We consider the number
. We consider the number 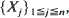 , and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of
, and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of 