Refine listing
Actions for selected content:
304 results in 60Cxx
A weakly 1-stable distribution for the number of random records and cuttings in split trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 151-177
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Generalized Coupon Collection: The Superlinear Case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 189-199
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Large Cliques in a Power-Law Random Graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1124-1135
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Critical epidemics, random graphs, and Brownian motion with a parabolic drift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1187-1206
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Gaussian phases in generalized coupon collection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 994-1012
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Extreme value theory, Poisson-Dirichlet distributions, and first passage percolation on random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 706-738
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Phases in the Diffusion of Gases via the Ehrenfest URN Modelx
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 841-855
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Recurrence Equations for the Probability Distribution of Sample Configurations in Exact Population Genetics Models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 732-751
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
On the number of runs for Bernoulli arrays
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 367-377
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
On the Variety of Shapes on the Fringe of a Random Recursive Tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 191-200
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
On Occurrences of F-S Strings in Linearly and Circularly Ordered Binary Sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 157-178
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
On the number of allelic types for samples taken from exchangeable coalescents with mutation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1082-1101
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
An Alternative Condition for Stochastic Domination
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1198-1200
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
The lying oracle game with a biased coin
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1023-1040
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Isomorphism and Symmetries in Random Phylogenetic Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1005-1019
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
On Consecutive Records in Certain Bernoulli Sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1201-1208
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Gaps in Discrete Random Samples
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1038-1051
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
On the probability of the existence of fixed-size components in random geometric graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 344-357
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Quasi-Birth-and-Death Processes, Lattice Path Counting, and Hypergeometric Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-520
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Necklace Processes Via Pólya Urns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 284-295
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
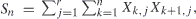 which denotes the number of consecutive pairs of successes (or runs of length 2) when reading the array down the columns and across the rows. With the case
which denotes the number of consecutive pairs of successes (or runs of length 2) when reading the array down the columns and across the rows. With the case 