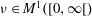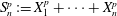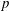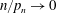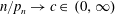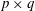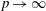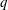Refine listing
Actions for selected content:
304 results in 60Cxx
On the Random Sampling of Pairs, with Pedestrian Examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 292-305
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Monotone Cellular Automata in a Random Environment
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 4 / July 2015
- Published online by Cambridge University Press:
- 02 February 2015, pp. 687-722
-
- Article
- Export citation
Λ-coalescents: a survey
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 23-40
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The front of the epidemic spread and first passage percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 101-121
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
How Clustering Affects Epidemics in Random Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 985-1008
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A Binomial Splitting Process in Connection with Corner Parking Problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 971-989
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Asymptotic hitting probabilities for the Bolthausen-Sznitman coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 87-97
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The probability that a random multigraph is simple. II
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 123-137
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Minimal Clade Size in the Bolthausen-Sznitman Coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 657-668
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
LIMIT THEOREMS FOR RADIAL RANDOM WALKS ON EUCLIDEAN SPACES OF HIGH DIMENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 212-236
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Optimal Online Selection of an Alternating Subsequence: A Central Limit Theorem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 536-559
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On Asymptotics of the Beta Coalescents
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 496-515
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Perpetuities in Fair Leader Election Algorithms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 203-216
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
The Number of Collisions for the Occupancy Problem with Unequal Probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 168-185
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Power Laws in Preferential Attachment Graphs and Stein's Method for the Negative Binomial Distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 876-893
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Joint Distribution of Distances in Large Random Regular Networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 861-870
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Overlap Problems on the Circle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 773-790
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Predecessors and Successors in Random Mappings with Exchangeable In-Degrees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 721-740
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Pruned Discrete Random Samples
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 542-556
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Phase Changes in the Topological Indices of Scale-Free Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 516-532
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation

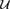

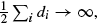 the probability that the multigraph is simple stays away from 0 if and only if
the probability that the multigraph is simple stays away from 0 if and only if 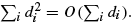 The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.
The new proof uses the method of moments, which makes it possible to use it in some applications concerning convergence in distribution. Corresponding results for bipartite graphs are included.