Refine listing
Actions for selected content:
304 results in 60Cxx
A Note on Embedding Certain Bernoulli Sequences in Marked Poisson Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1181-1185
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Run Statistics Defined on the Multicolor URN Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1007-1023
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Expected coalescence time for a nonuniform allocation process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1002-1032
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On Asymptotics of Exchangeable Coalescents with Multiple Collisions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1186-1195
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Random Permutation Model Arising in Chemistry
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1060-1070
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Average-Case Analysis of Cousins in m-ary Tries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 888-900
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
The Number of Two Consecutive Successes in a Hoppe-Pólya Urn
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-906
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
A Poisson Approximation for an Occupancy Problem with Collisions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 430-439
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
On Negative Binomial Approximation to k-Runs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 456-471
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Poisson Approximation for the Number of Repeats in a Stationary Markov Chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 440-455
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
The Necklace Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 271-278
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Local properties of random mappings with exchangeable in-degrees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 183-205
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Distributions of the Longest Excursions in a Tied Down Simple Random Walk and in a Brownian Bridge
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1056-1067
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Success run statistics defined on an urn model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 991-1019
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Graphs with specified degree distributions, simple epidemics, and local vaccination strategies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 922-948
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Counts of Failure Strings in Certain Bernoulli Sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 824-830
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Identities linking volumes of convex hulls
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 630-644
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Improved compound Poisson approximation for the number of occurrences of any rare word family in a stationary markov chain
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 128-140
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Parallel matching for ranking all teams in a tournament
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 804-826
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Limit distribution of distances in biased random tries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 377-390
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
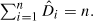 In the random digraph,
In the random digraph, 