Refine listing
Actions for selected content:
304 results in 60Cxx
Shape Measures of Random Increasing k-trees†
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 04 May 2016, pp. 668-699
-
- Article
- Export citation
Multivariate Eulerian Polynomials and Exclusion Processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 18 March 2016, pp. 486-499
-
- Article
- Export citation
The degree profile and weight in Apollonian networks and k-trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 163-175
- Print publication:
- March 2016
-
- Article
- Export citation
Coexistence in Preferential Attachment Networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 09 February 2016, pp. 797-822
-
- Article
- Export citation
Probabilistic Divide-and-Conquer: A New Exact Simulation Method, With Integer Partitions as an Example
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 324-351
-
- Article
- Export citation
Contagions in random networks with overlapping communities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 973-988
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On degenerate sums of m-dependent variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1146-1155
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On a generalization of a waiting time problem and some combinatorial identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 981-989
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Convergence of Achlioptas Processes via Differential Equations with Unique Solutions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 14 October 2015, pp. 154-171
-
- Article
- Export citation
Reversible Markov structures on divisible set partitions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 622-635
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Distance between two random k-out digraphs, with and without preferential attachment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 858-879
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
On the Method of Typical Bounded Differences
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 27 August 2015, pp. 269-299
-
- Article
- Export citation
A Sharp Uniform Bound for the Distribution of Sums of Bernoulli Trials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 07 July 2015, pp. 352-361
-
- Article
- Export citation
New Results on a Generalized Coupon Collector Problem Using Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 405-418
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
The Kruskal-Katona Theorem and a Characterization of System Signatures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 508-518
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
DYADIC SHIFT RANDOMIZATION IN CLASSICAL DISCREPANCY THEORY
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 06 May 2015, pp. 183-209
- Print publication:
- 2016
-
- Article
- Export citation
Asymptotic Properties of Protected Nodes in Random Recursive Trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 290-297
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Maximal Percentages in Pólya's Urn
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 180-190
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Infection Spread in Random Geometric Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 164-181
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
The Mixing Time of the Newman-Watts Small-World Model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 37-56
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
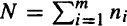 Let
Let 
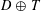
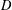
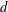
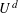
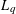
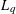
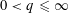
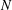
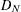
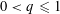
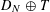
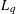
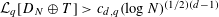
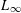
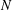
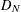
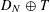
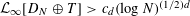
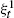 starting with all nodes infected survives up to time
starting with all nodes infected survives up to time 