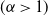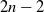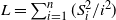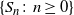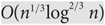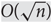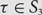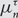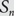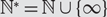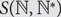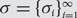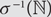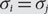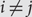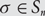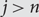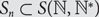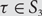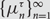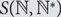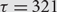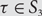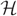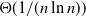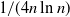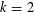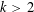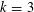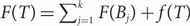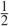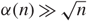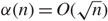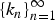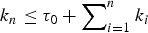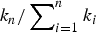Refine listing
Actions for selected content:
304 results in 60Cxx
Preferential attachment when stable
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 November 2019, pp. 1067-1108
- Print publication:
- December 2019
-
- Article
- Export citation
The string of diamonds is nearly tight for rumour spreading
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 190-199
-
- Article
- Export citation
Unlabelled Gibbs partitions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 293-309
-
- Article
- Export citation
YANG–BAXTER FIELD FOR SPIN HALL–LITTLEWOOD SYMMETRIC FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e39
-
- Article
-
- You have access
- Open access
- Export citation
On the Brownian separable permuton
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 24 October 2019, pp. 241-266
-
- Article
- Export citation
The Infinite limit of random permutations avoiding patterns of length three
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 October 2019, pp. 137-152
-
- Article
- Export citation
Positive association of the oriented percolation cluster in randomly oriented graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 08 July 2019, pp. 811-815
-
- Article
- Export citation
A natural barrier in random greedy hypergraph matching
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 27 June 2019, pp. 816-825
-
- Article
- Export citation
An Improved Upper Bound for Bootstrap Percolation in All Dimensions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 17 June 2019, pp. 936-960
-
- Article
- Export citation
On the rate of convergence for the length of the longest common subsequences in hidden Markov models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 558-573
- Print publication:
- June 2019
-
- Article
- Export citation
Accessibility percolation on random rooted labeled trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 30 July 2019, pp. 533-545
- Print publication:
- June 2019
-
- Article
- Export citation
The sharp threshold for jigsaw percolation in random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 378-407
- Print publication:
- June 2019
-
- Article
- Export citation
A PROOF OF ANDREWS’ CONJECTURE ON PARTITIONS WITH NO SHORT SEQUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 30 May 2019, e17
-
- Article
-
- You have access
- Open access
- Export citation
A central limit theorem for additive functionals of increasing trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 618-637
-
- Article
- Export citation
The spread of fire on a random multigraph
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 1-40
- Print publication:
- March 2019
-
- Article
- Export citation
A conditional Berry–Esseen inequality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 76-90
- Print publication:
- March 2019
-
- Article
- Export citation
THE GENERALIZED ENTROPY ERGODIC THEOREM FOR NONHOMOGENEOUS MARKOV CHAINS INDEXED BY A HOMOGENEOUS TREE
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 221-234
-
- Article
- Export citation
A SPECTRUM OF SERIES–PARALLEL GRAPHS WITH MULTIPLE EDGE EVOLUTION
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 487-499
-
- Article
- Export citation
A Linear Threshold for Uniqueness of Solutions to Random Jigsaw Puzzles
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 08 January 2019, pp. 287-302
-
- Article
-
- You have access
- Export citation
Random systems in ultrametric spaces
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 83-97
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation