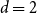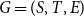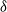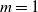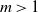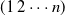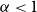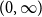Refine listing
Actions for selected content:
304 results in 60Cxx
Uniqueness of the Gibbs measure for the 4-state anti-ferromagnetic Potts model on the regular tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 07 September 2022, pp. 158-182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On connectivity and robustness of random graphs with inhomogeneity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 284-294
- Print publication:
- March 2023
-
- Article
- Export citation
A BK inequality for random matchings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 July 2022, pp. 151-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local weak limit and subgraph counts for sparse random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 July 2022, pp. 755-776
- Print publication:
- September 2022
-
- Article
- Export citation
The shape of a seed bank tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 June 2022, pp. 631-651
- Print publication:
- September 2022
-
- Article
- Export citation
Giant descendant trees, matchings, and independent sets in age-biased attachment graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 299-324
- Print publication:
- June 2022
-
- Article
- Export citation
Refined universality for critical KCM: lower bounds
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 879-906
-
- Article
- Export citation
Random stable-type minimal factorizations of the n-cycle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 24 February 2022, pp. 1-63
- Print publication:
- March 2022
-
- Article
- Export citation
Unusually large components in near-critical Erdős–Rényi graphs via ballot theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 840-869
-
- Article
- Export citation
A note on the Screaming Toes game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 118-130
- Print publication:
- March 2022
-
- Article
- Export citation
The containment profile of hyper-recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 278-296
- Print publication:
- March 2022
-
- Article
- Export citation
Exchangeable and sampling-consistent distributions on rooted binary trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 14 January 2022, pp. 60-80
- Print publication:
- March 2022
-
- Article
- Export citation
Random intersection graphs with communities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1061-1089
- Print publication:
- December 2021
-
- Article
- Export citation
Sequential metric dimension for random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 909-951
- Print publication:
- December 2021
-
- Article
- Export citation
Arcsine laws for random walks generated from random permutations with applications to genomics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 851-867
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
A restaurant process with cocktail bar and relations to the three-parameter Mittag–Leffler distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 978-1006
- Print publication:
- December 2021
-
- Article
- Export citation
Covariances in Pólya urn schemes
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 October 2021, pp. 60-71
-
- Article
- Export citation
On the number of Hadamard matrices via anti-concentration
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 455-477
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The distance profile of rooted and unrooted simply generated trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 18 August 2021, pp. 368-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combinatorial anti-concentration inequalities, with applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 30 June 2021, pp. 227-248
- Print publication:
- September 2021
-
- Article
- Export citation