Refine listing
Actions for selected content:
528 results in 60Exx
A new ordering for stochastic majorization: theory and applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 604-634
- Print publication:
- September 1992
-
- Article
- Export citation
On measures of non-degeneracy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 733-739
- Print publication:
- September 1992
-
- Article
- Export citation
A stochastic ordering of partial sums of independent random variables and of some random processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 645-654
- Print publication:
- September 1992
-
- Article
- Export citation
Extension of the bivariate characterization for stochastic orders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 506-508
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
The abscissa of convergence of the Laplace transform
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 353-362
- Print publication:
- June 1992
-
- Article
- Export citation
Analysis of the Luria–Delbrück distribution using discrete convolution powers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 255-267
- Print publication:
- June 1992
-
- Article
- Export citation
A finite form for the wrapped Poisson distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 221-222
- Print publication:
- March 1992
-
- Article
-
- You have access
- Export citation
Stochastic convexity of sums of i.i.d. non-negative random variables with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 156-167
- Print publication:
- March 1992
-
- Article
- Export citation
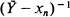 where
where 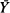 is the mean of the sample values overshooting
is the mean of the sample values overshooting 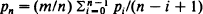 where
where 