Refine listing
Actions for selected content:
524 results in 60Exx
Stochastic monotonicity and conditional Monte Carlo for likelihood ratios
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 103-115
- Print publication:
- March 1993
-
- Article
- Export citation
On the optimal control of cancer radiotherapy for non-homogeneous cell populations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-23
- Print publication:
- March 1993
-
- Article
- Export citation
An unusual stochastic order relation with some applications in sampling and epidemic theory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 63-81
- Print publication:
- March 1993
-
- Article
- Export citation
Extremal properties of the FIFO discipline in queueing networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 967-978
- Print publication:
- December 1992
-
- Article
- Export citation
Stochastic comparisons for queueing models via random sums and intervals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 960-985
- Print publication:
- December 1992
-
- Article
- Export citation
Further monotonicity properties of renewal processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 575-588
- Print publication:
- September 1992
-
- Article
- Export citation
A new ordering for stochastic majorization: theory and applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 604-634
- Print publication:
- September 1992
-
- Article
- Export citation
On measures of non-degeneracy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 733-739
- Print publication:
- September 1992
-
- Article
- Export citation
A stochastic ordering of partial sums of independent random variables and of some random processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 645-654
- Print publication:
- September 1992
-
- Article
- Export citation
Extension of the bivariate characterization for stochastic orders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 506-508
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
The abscissa of convergence of the Laplace transform
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 353-362
- Print publication:
- June 1992
-
- Article
- Export citation
Analysis of the Luria–Delbrück distribution using discrete convolution powers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 255-267
- Print publication:
- June 1992
-
- Article
- Export citation
A finite form for the wrapped Poisson distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 221-222
- Print publication:
- March 1992
-
- Article
-
- You have access
- Export citation
Stochastic convexity of sums of i.i.d. non-negative random variables with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 156-167
- Print publication:
- March 1992
-
- Article
- Export citation
Second order subexponential distributions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-87
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Factorization of probability measures on symmetric hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 417-467
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
A note on the Lévy-Khinchin representation of negative definite functions on Hilbert spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 104-116
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
Convolutions of Distributions With Exponential and Subexponential Tails
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-365
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
Rearranging measures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 1 / February 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-30
- Print publication:
- February 1983
-
- Article
-
- You have access
- Export citation
Attainable bounds for expectations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-420
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
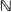 -valued random variables, unusual in the literature, based on the descending factorial moments. Further applications of the ordering occur when comparing certain sampling procedures through the number of un-sampled individuals. In particular, it is used to reinforce slightly comparison results obtained earlier for two such samplings.
-valued random variables, unusual in the literature, based on the descending factorial moments. Further applications of the ordering occur when comparing certain sampling procedures through the number of un-sampled individuals. In particular, it is used to reinforce slightly comparison results obtained earlier for two such samplings.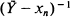 where
where 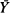 is the mean of the sample values overshooting
is the mean of the sample values overshooting 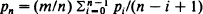 where
where  and use their properties to give a proof of the Lévy-Khinchin formula for an infinitely divisible probability distribution on
and use their properties to give a proof of the Lévy-Khinchin formula for an infinitely divisible probability distribution on 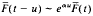 and
and 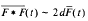 as
as 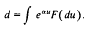 .
.