Refine listing
Actions for selected content:
524 results in 60Exx
Stochastic Orders Generated by Integrals: a Unified Study
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 414-428
- Print publication:
- June 1997
-
- Article
- Export citation
The product of independent random variables with slowly varying truncated moments
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 186-197
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
Compound Poisson limit theorems for Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 24-34
- Print publication:
- March 1997
-
- Article
- Export citation
Variants of the Choquet–Deny theorem with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 101-106
- Print publication:
- March 1997
-
- Article
- Export citation
Some majorization orderings of heterogeneity in a class of epidemics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 84-93
- Print publication:
- March 1997
-
- Article
- Export citation
Shapes of Rectangular Prisms After Repeated Random Division
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 26-37
- Print publication:
- March 1997
-
- Article
- Export citation
Properties of moments for s-order equilibrium distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1108-1111
- Print publication:
- December 1996
-
- Article
- Export citation
On identifiability and order of continuous-time aggregated Markov chains, Markov-modulated Poisson processes, and phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 640-653
- Print publication:
- September 1996
-
- Article
- Export citation
Stein's method for geometric approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 707-713
- Print publication:
- September 1996
-
- Article
- Export citation
Comparing sums of exchangeable Bernoulli random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 285-310
- Print publication:
- September 1996
-
- Article
- Export citation
On closure of some partial orderings under mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 698-706
- Print publication:
- September 1996
-
- Article
- Export citation
Randomized multihit models and their identification
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 458-471
- Print publication:
- September 1996
-
- Article
- Export citation
A note on disjoint-occurrence inequalities for marked Poisson point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 420-426
- Print publication:
- September 1996
-
- Article
- Export citation
Multivariate Bonferroni-type lower bounds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 729-740
- Print publication:
- September 1996
-
- Article
- Export citation
Perpetuities with thin tails
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 463-480
- Print publication:
- June 1996
-
- Article
- Export citation
Poisson and compound Poisson approximations for random sums of random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 127-137
- Print publication:
- March 1996
-
- Article
- Export citation
An operational calculus for probability distributions via Laplace transforms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 75-113
- Print publication:
- March 1996
-
- Article
- Export citation
Bonferroni inequalities and deviations of discrete distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-121
- Print publication:
- March 1996
-
- Article
- Export citation
Distributions and expectations of singular random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1032-1040
- Print publication:
- December 1995
-
- Article
- Export citation
Characterization of a general class of life-testing models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 548-553
- Print publication:
- June 1995
-
- Article
- Export citation
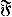 be a class of functions and let
be a class of functions and let 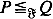 , if ∫ ⨍
, if ∫ ⨍ 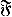 . Marshall (1991) posed the problem of characterizing the maximal cone of functions generating such an ordering. We solve this problem by using methods from functional analysis. Another purpose of this paper is to derive properties of such
. Marshall (1991) posed the problem of characterizing the maximal cone of functions generating such an ordering. We solve this problem by using methods from functional analysis. Another purpose of this paper is to derive properties of such 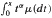 ) are investigated. Maller shows that if
) are investigated. Maller shows that if 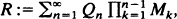 where
where 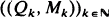 is an independent, identically distributed sequence with
is an independent, identically distributed sequence with 