Refine listing
Actions for selected content:
524 results in 60Exx
On the variance to mean ratio for random variables from Markov chains and point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 303-312
- Print publication:
- June 1998
-
- Article
- Export citation
On Reliability Bounds via Conditional Inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 104-114
- Print publication:
- March 1998
-
- Article
- Export citation
Characterizations of the Exponential Distribution via the Blocking Time in a Queueing System with an Unreliable Server
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 236-239
- Print publication:
- March 1998
-
- Article
- Export citation
Multivariate Convex Orderings, Dependence, and Stochastic Equality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 93-103
- Print publication:
- March 1998
-
- Article
- Export citation
Non-Gaussian Density Processes Arising from Non-Poisson Systems of Independent Brownian Motions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 213-220
- Print publication:
- March 1998
-
- Article
- Export citation
Preservation of multivariate stochastic orders under multivariate Poisson shock models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1009-1020
- Print publication:
- December 1997
-
- Article
- Export citation
On the rate of Poisson process approximation to a Bernoulli process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 898-907
- Print publication:
- December 1997
-
- Article
- Export citation
The moments of FIND
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1079-1082
- Print publication:
- December 1997
-
- Article
- Export citation
A Stochastic Model of Carcinogenesis and Tumor Size at Detection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 607-628
- Print publication:
- September 1997
-
- Article
- Export citation
Coherent structures and unimodality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 812-817
- Print publication:
- September 1997
-
- Article
- Export citation
Sooner waiting time problems in a sequence of trinary trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 593-609
- Print publication:
- September 1997
-
- Article
- Export citation
Characterization of life distributions under some generalized stochastic orderings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 711-719
- Print publication:
- September 1997
-
- Article
- Export citation
Laplace transforms and the renewal equation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 395-403
- Print publication:
- June 1997
-
- Article
- Export citation
Asymptotic Expansions in the Exponent: a Compound Poisson Approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 374-387
- Print publication:
- June 1997
-
- Article
- Export citation
Bounds for the Joint Survival and Incidence Functions Through Coherent System Data
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 478-497
- Print publication:
- June 1997
-
- Article
- Export citation
Integral Probability Metrics and Their Generating Classes of Functions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 429-443
- Print publication:
- June 1997
-
- Article
- Export citation
Moment inequalities for sums of DMRL random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 525-535
- Print publication:
- June 1997
-
- Article
- Export citation
Stochastic comparisons of random minima and maxima
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 420-425
- Print publication:
- June 1997
-
- Article
- Export citation
Stochastic orders based on ratios of Laplace transforms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 404-419
- Print publication:
- June 1997
-
- Article
- Export citation
On the time a Markov chain spends in a lumped state
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 340-345
- Print publication:
- June 1997
-
- Article
- Export citation
 of functions and probability measures
of functions and probability measures 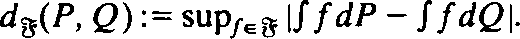 A unified study of such
A unified study of such 