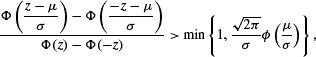Refine listing
Actions for selected content:
524 results in 60Exx
Probabilistic aspects of the SU(2)-harmonic oscillator
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 306-314
- Print publication:
- March 2000
-
- Article
- Export citation
Compound Poisson approximation for the Johnson-Mehl model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 101-117
- Print publication:
- March 2000
-
- Article
- Export citation
Four interesting problems concerning Markovian shape sequences
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 954-968
- Print publication:
- December 1999
-
- Article
- Export citation
On the occurrence of composite events and clusters of points
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1012-1018
- Print publication:
- December 1999
-
- Article
- Export citation
A unified approach to the study of tail probabilities of compound distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1058-1073
- Print publication:
- December 1999
-
- Article
- Export citation
Stochastic properties of a cumulative damage threshold crossing model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 720-732
- Print publication:
- September 1999
-
- Article
- Export citation
Poisson process via martingale and related characteristics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 919-926
- Print publication:
- September 1999
-
- Article
- Export citation
Mass transportation problems with capacity constraints
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 433-445
- Print publication:
- June 1999
-
- Article
- Export citation
Stochastic orders in preservation properties by Bernstein-type operators
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 492-509
- Print publication:
- June 1999
-
- Article
- Export citation
Simpson-type paradoxes, dependence, and ageing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 119-131
- Print publication:
- March 1999
-
- Article
- Export citation
On an inequality for the normal distribution arising in bioequivalence studies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 279-286
- Print publication:
- March 1999
-
- Article
- Export citation
Exact distribution of word occurrences in a random sequence of letters
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 179-193
- Print publication:
- March 1999
-
- Article
- Export citation
Invariant distributions for shapes in sequences of randomly-divided rectangles
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-14
- Print publication:
- March 1999
-
- Article
- Export citation
A probabilistic proof of Stein's factors
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 287-290
- Print publication:
- March 1999
-
- Article
- Export citation
Un principe d'invariance pour une classe de marches p-corrélées sur ℤd
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 557-565
- Print publication:
- September 1998
-
- Article
- Export citation
Random nested tetrahedra
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 619-627
- Print publication:
- September 1998
-
- Article
- Export citation
On mixture representation of the Linnik density
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-326
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Optimal lower bounds for bivariate probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 476-492
- Print publication:
- June 1998
-
- Article
- Export citation
Optimal and myopic search in a binary random vector
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 463-472
- Print publication:
- June 1998
-
- Article
- Export citation
Absorption sampling and the absorption distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 489-494
- Print publication:
- June 1998
-
- Article
- Export citation