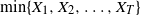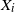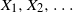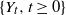Refine listing
Actions for selected content:
528 results in 60Exx
Bivariate shock models driven by the geometric counting process
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 12 February 2026, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graphical sequences and plane trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 05 February 2026, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Any random variable with right-unbounded distributional support is the minimum of independent and very heavy-tailed random variables
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-10
-
- Article
- Export citation
Quantifying stochastic dependence of marginal lifetimes of two-component load-sharing parallel systems
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 13 January 2026, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Negative dependence in knockout tournaments
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-16
-
- Article
- Export citation
Infinitely resizable urn models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-35
-
- Article
- Export citation
The distribution of the minimum observation until a stopping time, with an application to the minimal spacing in a Renewal process
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local central limit theorem for triangle counts in sparse random graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 14 November 2025, pp. 459-475
- Print publication:
- March 2026
-
- Article
- Export citation
Quantization dimensions of negative order
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 11 November 2025, pp. 433-457
- Print publication:
- March 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral stochastic orders with parametric classes of functions
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-31
-
- Article
- Export citation
A TRACTABLE SYMMETRIC MULTIVARIATE LOGISTIC DISTRIBUTION WITH BOUNDED SCORE FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-7
-
- Article
- Export citation
Generalized equilibrium distributions
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 40 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 31 July 2025, pp. 63-89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse clustering of Gibbs partitions via independent fragmentation and dual dependent coagulation operators
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 30 July 2025, pp. 1-18
-
- Article
- Export citation
Relative entropy bounds for sampling with and without replacement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1578-1593
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comparisons of variances through the probabilistic mean value theorem and applications
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 15 July 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rates for the SLLN for long-memory and heavy-tailed processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1513-1533
- Print publication:
- December 2025
-
- Article
- Export citation
The replicator coalescent
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1534-1548
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stein’s method for distributions modelling competing and complementary risk problems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 1510-1538
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable functional CLT for deterministic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3192-3222
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radially geometric stable distributions and processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 10 April 2025, pp. 1392-1429
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation