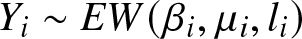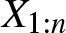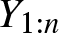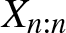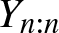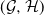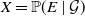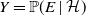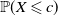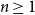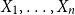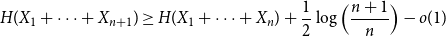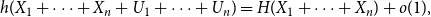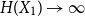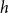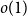Refine listing
Actions for selected content:
524 results in 60Exx
Barlow and Proschan principle for coherent systems with statistically dependent component and redundancy lifetimes
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 141-155
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new weighted means of failure rate and associated quantile versions
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 64-82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STABILITY ANALYSIS FOR STOCHASTIC MCKEAN–VLASOV EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 06 November 2024, e6
-
- Article
- Export citation
Majorization and randomness measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 16 October 2024, pp. 541-557
- Print publication:
- June 2025
-
- Article
- Export citation
The impact of pinning points on memorylessness in Lévy random bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 15 October 2024, pp. 172-187
- Print publication:
- March 2025
-
- Article
- Export citation
On the rate of convergence for an α-stable central limit theorem under sublinear expectation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 209-233
- Print publication:
- March 2025
-
- Article
- Export citation
Tail variance and confidence of using tail conditional expectation: Analytical representation, capital adequacy, and asymptotics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 July 2024, pp. 346-369
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bivariate tempered space-fractional Poisson process and shock models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1485-1501
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orderings of extremes among dependent extended Weibull random variables
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 07 May 2024, pp. 705-732
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A remark on exact simulation of tempered stable Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1196-1198
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
A remark on a conjecture on the symmetric Gaussian problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 643-661
-
- Article
- Export citation
Coherent distributions on the square–extreme points and asymptotics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1240-1262
- Print publication:
- December 2024
-
- Article
- Export citation
Skew Ornstein–Uhlenbeck processes with sticky reflection and their applications to bond pricing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1172-1195
- Print publication:
- December 2024
-
- Article
- Export citation
Connectivity of random graphs after centrality-based vertex removal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 967-998
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some semi-parametric estimates for European option prices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 999-1009
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Log-concavity and relative log-concave ordering of compound distributions
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 579-593
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CUMULATIVE DISTRIBUTION FUNCTION OF THE VARIANCE-GAMMA DISTRIBUTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 389-397
- Print publication:
- October 2024
-
- Article
- Export citation
Approximate discrete entropy monotonicity for log-concave sums
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 196-209
-
- Article
- Export citation
Characteristics of the switch process and geometric divisibility
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 802-809
- Print publication:
- September 2024
-
- Article
- Export citation
Aging notions, stochastic orders, and expected utilities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 767-780
- Print publication:
- September 2024
-
- Article
- Export citation