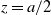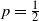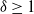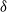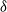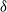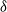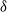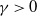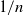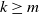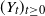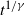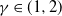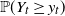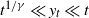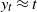Refine listing
Actions for selected content:
524 results in 60Exx
Stochastic ordering results on the duration of the gambler’s ruin game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 603-621
- Print publication:
- June 2024
-
- Article
- Export citation
Preservation of mean inactivity time ordering for coherent systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 666-692
- Print publication:
- June 2024
-
- Article
- Export citation
Exchangeable FGM copulas
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 205-234
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An elementary approach to the inverse first-passage-time problem for soft-killed Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 279-300
- Print publication:
- March 2024
-
- Article
- Export citation
Ordering and ageing properties of developed sequential order statistics governed by the Archimedean copula
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 464-494
- Print publication:
- June 2024
-
- Article
- Export citation
Distributions of random variables involved in discrete censored δ-shock models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1144-1170
- Print publication:
- December 2023
-
- Article
- Export citation
Distribution of consensus in a broadcast-based consensus algorithm with random initial opinions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 May 2023, pp. 1416-1438
- Print publication:
- December 2023
-
- Article
- Export citation
Asymptotic results on tail moment and tail central moment for dependent risks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 08 May 2023, pp. 1116-1143
- Print publication:
- December 2023
-
- Article
- Export citation
Stochastic comparison on active redundancy allocation to K-out-of-N systems with statistically dependent component and redundancy lifetimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 1085-1115
- Print publication:
- December 2023
-
- Article
- Export citation
Stochastic comparisons of largest claim and aggregate claim amounts
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 245-267
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Bruss–Robertson–Steele inequality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 1112-1114
- Print publication:
- September 2023
-
- Article
- Export citation
A new lifetime distribution by maximizing entropy: properties and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 February 2023, pp. 189-206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cumulant transforms for Hawkes processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 528-541
- Print publication:
- June 2023
-
- Article
- Export citation
Exactly solvable urn models under random replacement schemes and their applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 835-854
- Print publication:
- September 2023
-
- Article
- Export citation
On Tournaments and negative dependence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 945-954
- Print publication:
- September 2023
-
- Article
- Export citation
The number of K-tons in the coupon collector problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 February 2023, pp. 723-736
- Print publication:
- September 2023
-
- Article
- Export citation
Competing risks and shock models governed by a generalized bivariate Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 709-722
- Print publication:
- June 2023
-
- Article
- Export citation
Optimal allocation of policy limits in layer reinsurance treaties
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 546-566
-
- Article
- Export citation
Large deviations of Poisson Telecom processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 October 2022, pp. 267-283
- Print publication:
- March 2023
-
- Article
- Export citation
Dispersive orderings induced by differences of inter risk measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 October 2022, pp. 358-365
- Print publication:
- March 2023
-
- Article
- Export citation