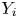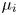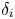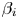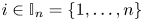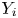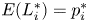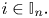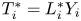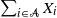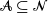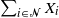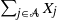Refine listing
Actions for selected content:
524 results in 60Exx
Ordering results for smallest claim amounts from two portfolios of risks with dependent heterogeneous exponentiated location-scale claims
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 26 July 2021, pp. 1116-1137
-
- Article
- Export citation
Exact simulation of Ornstein–Uhlenbeck tempered stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 347-371
- Print publication:
- June 2021
-
- Article
- Export citation
Stochastic orderings of multivariate elliptical distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 551-568
- Print publication:
- June 2021
-
- Article
- Export citation
Concentration functions and entropy bounds for discrete log-concave distributions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 54-72
-
- Article
- Export citation
Stochastic comparison of parallel systems with Pareto components
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 20 May 2021, pp. 950-962
-
- Article
- Export citation
Log-concavity and log-convexity of moments of averages of i.i.d. random variables
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 271-278
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Can Coherent Predictions be Contradictory?
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 133-161
- Print publication:
- March 2021
-
- Article
- Export citation
Tail asymptotics of an infinitely divisible space-time model with convolution equivalent Lévy measure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 42-67
- Print publication:
- March 2021
-
- Article
- Export citation
Stochastic comparisons and ageing properties of an extended gamma process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 140-163
- Print publication:
- March 2021
-
- Article
- Export citation
The martingale comparison method for Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 164-176
- Print publication:
- March 2021
-
- Article
- Export citation
On a generalization of the Rényi–Srivastava characterization of the Poisson law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 68-82
- Print publication:
- March 2021
-
- Article
- Export citation
EXACT LOWER BOUND ON AN ‘EXACTLY ONE’ PROBABILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 23 February 2021, pp. 330-336
- Print publication:
- October 2021
-
- Article
- Export citation
Draw-down Parisian ruin for spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1164-1196
- Print publication:
- December 2020
-
- Article
- Export citation
Multivariate finite-support phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1260-1275
- Print publication:
- December 2020
-
- Article
- Export citation
Non-Comparability with respect to the convex transform order with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1339-1348
- Print publication:
- December 2020
-
- Article
- Export citation
CONTRIBUTIONS TO ESTIMATION AND MODELING USING QUANTILES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 523-524
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Explicit results on conditional distributions of generalized exponential mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 760-774
- Print publication:
- September 2020
-
- Article
- Export citation
On moderate deviations in Poisson approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 1005-1027
- Print publication:
- September 2020
-
- Article
- Export citation
Stochastic comparisons of largest-order statistics for proportional reversed hazard rate model and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 September 2020, pp. 832-852
- Print publication:
- September 2020
-
- Article
- Export citation
SECOND ORDER SUBEXPONENTIALITY AND INFINITE DIVISIBILITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 367-390
- Print publication:
- June 2022
-
- Article
- Export citation