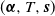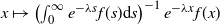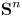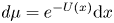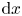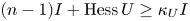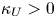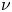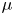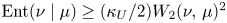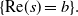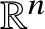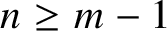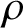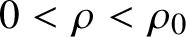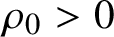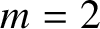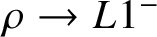Refine listing
Actions for selected content:
524 results in 60Exx
A Markov jump process associated with the matrix-exponential distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 1-13
- Print publication:
- March 2023
-
- Article
- Export citation
Transportation on spheres via an entropy formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1467-1478
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gromov–Wasserstein distances between Gaussian distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1178-1198
- Print publication:
- December 2022
-
- Article
- Export citation
Almost first-order stochastic dominance by distorted expectations
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 12 August 2022, pp. 888-906
-
- Article
- Export citation
Construction of aggregation paradoxes through load-sharing models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 223-244
- Print publication:
- March 2023
-
- Article
- Export citation
Dynamical fitness models: evidence of universality classes for preferential attachment graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 609-630
- Print publication:
- September 2022
-
- Article
- Export citation
Non-asymptotic control of the cumulative distribution function of Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 913-944
- Print publication:
- September 2022
-
- Article
- Export citation
Exponential and gamma form for tail expansions of first-passage distributions in semi-markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1291-1319
- Print publication:
- December 2022
-
- Article
- Export citation
Unified signature cumulants and generalized Magnus expansions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Further properties of fractional stochastic dominance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 March 2022, pp. 202-223
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On reconsidering entropies and divergences and their cumulative counterparts: Csiszár's, DPD's and Fisher's type cumulative and survival measures
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 February 2022, pp. 294-321
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How a probabilistic analogue of the mean value theorem yields stein-type covariance identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 350-365
- Print publication:
- June 2022
-
- Article
- Export citation
On transform orders for largest claim amounts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1064-1085
- Print publication:
- December 2021
-
- Article
- Export citation
Optimal allocation of relevations in coherent systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1152-1169
- Print publication:
- December 2021
-
- Article
- Export citation
Bounds on the mean and squared coefficient of variation of phase-type distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 880-889
- Print publication:
- December 2021
-
- Article
- Export citation
Three candidate plurality is stablest for small correlations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 September 2021, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ordering and aging properties of systems with dependent components governed by the Archimedean copula
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 17 September 2021, pp. 1-28
-
- Article
- Export citation
Estimating tails of independently stopped random walks using concave approximations of hazard functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 773-793
- Print publication:
- September 2021
-
- Article
- Export citation
Stochastic ordering for birth–death processes with killing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 708-720
- Print publication:
- September 2021
-
- Article
- Export citation
Stochastic properties of generalized finite mixture models with dependent components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 794-804
- Print publication:
- September 2021
-
- Article
- Export citation