Refine listing
Actions for selected content:
524 results in 60Exx
Approximations of small jumps of Lévy processes with a view towards simulation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 482-493
- Print publication:
- June 2001
-
- Article
- Export citation
On the closure of the IFR(2) and NBU(2) classes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 235-241
- Print publication:
- March 2001
-
- Article
- Export citation
On the nature of the binomial distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 36-44
- Print publication:
- March 2001
-
- Article
- Export citation
Monotone Markov processes with respect to the reversed hazard rate ordering: an application to reliability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 195-208
- Print publication:
- March 2001
-
- Article
- Export citation
The travel time in carousel systems under the nearest item heuristic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 45-54
- Print publication:
- March 2001
-
- Article
- Export citation
Multivariate subordination, self-decomposability and stability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 160-187
- Print publication:
- March 2001
-
- Article
- Export citation
The moment index of minima
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 33-36
- Print publication:
- 2001
-
- Article
- Export citation
Simple ratio prophet inequalities for a mortal with multiple choices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1084-1091
- Print publication:
- December 2000
-
- Article
- Export citation
Stein factor bounds for random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1181-1187
- Print publication:
- December 2000
-
- Article
- Export citation
On s-convex approximations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 994-1010
- Print publication:
- December 2000
-
- Article
- Export citation
Convolutions of heavy-tailed random variables and applications to portfolio diversification and MA(1) time series
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1011-1026
- Print publication:
- December 2000
-
- Article
- Export citation
Some new results on stochastic comparisons of parallel systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1123-1128
- Print publication:
- December 2000
-
- Article
- Export citation
Generalized reliability bounds for coherent structures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 778-794
- Print publication:
- September 2000
-
- Article
- Export citation
Reduction techniques for discrete-time Markov chains on totally ordered state space using stochastic comparisons
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 795-806
- Print publication:
- September 2000
-
- Article
- Export citation
Joint distributions of successes, failures and patterns in enumeration problems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 866-884
- Print publication:
- September 2000
-
- Article
- Export citation
On some waiting time problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 756-764
- Print publication:
- September 2000
-
- Article
- Export citation
Poisson approximations for conditional r-scan lengths of multiple renewal processes and application to marker arrays in biomolecular sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 865-880
- Print publication:
- September 2000
-
- Article
- Export citation
Taylor's formula and preservation of generalized convexity for positive linear operators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 765-777
- Print publication:
- September 2000
-
- Article
- Export citation
On the waiting time in a janken game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 601-605
- Print publication:
- June 2000
-
- Article
- Export citation
A refinement of multivariate Bonferroni-type inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 276-282
- Print publication:
- March 2000
-
- Article
- Export citation
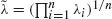 . Let
. Let 