Refine listing
Actions for selected content:
524 results in 60Exx
Student processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 342-365
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Level Crossing Ordering of Skip-Free-to-the-Right Continuous-Time Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 52-60
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Preservation of positive and negative orthant dependence concepts under mixtures and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 961-974
- Print publication:
- December 2004
-
- Article
- Export citation
Path reversal, islands, and the gapped alignment of random sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 975-983
- Print publication:
- December 2004
-
- Article
- Export citation
Infinite divisibility of infinite sums of lower records: a simple proof
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1187-1190
- Print publication:
- December 2004
-
- Article
- Export citation
Stochastic properties of the linear multifractional stable motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1085-1115
- Print publication:
- December 2004
-
- Article
- Export citation
A study of the Hartman–Watson distribution motivated by numerical problems related to the pricing of Asian options
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1049-1058
- Print publication:
- December 2004
-
- Article
- Export citation
Poisson approximation for (k 1, k 2)-events via the Stein-Chen method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1081-1092
- Print publication:
- December 2004
-
- Article
- Export citation
Distribution of the amount of genetic material from a chromosomal segment surviving to the following generation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 345-354
- Print publication:
- June 2004
-
- Article
- Export citation
Comparison of multivariate risks and positive dependence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-406
- Print publication:
- June 2004
-
- Article
- Export citation
Maximum dynamic entropy models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 379-390
- Print publication:
- June 2004
-
- Article
- Export citation
Numerical inversion for Laplace transforms of functions with discontinuities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 616-642
- Print publication:
- June 2004
-
- Article
- Export citation
Convolution equivalence and infinite divisibility
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 407-424
- Print publication:
- June 2004
-
- Article
- Export citation
Series representation and simulation of multifractional Lévy motions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 171-197
- Print publication:
- March 2004
-
- Article
- Export citation
The stochastic precedence ordering with applications in sampling and testing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 73-82
- Print publication:
- March 2004
-
- Article
- Export citation
On the rate of Poisson process approximation to a Bernoulli process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 271-276
- Print publication:
- March 2004
-
- Article
- Export citation
Correction to a paper by A. G. Pakes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 67-74
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
Fitting the variance-gamma model to financial data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 177-187
- Print publication:
- 2004
-
- Article
- Export citation
A mosaic of triangular cells formed with sequential splitting rules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 3-15
- Print publication:
- 2004
-
- Article
- Export citation
Stieltjes classes for moment-indeterminate probability distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 281-294
- Print publication:
- 2004
-
- Article
- Export citation
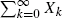 is equal in distribution to
is equal in distribution to 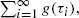 where {
where {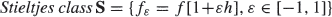 , where
, where 