Refine listing
Actions for selected content:
524 results in 60Exx
Stationary-increment Student and variance-gamma processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 441-453
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Limit Theorems for Moving Averages with Random Coefficients and Heavy-Tailed Noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 245-256
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Asymptotic behavior of a general class of mixture failure rates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 244-262
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
On regular variation for infinitely divisible random vectors and additive processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 134-148
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Compound Poisson Approximation Inequality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 282-288
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Positive Dependence and Weak Convergence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 48-59
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Waiting time distributions of competing patterns in higher-order Markovian sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 977-988
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Level-crossing ordering of semi-Markov processes and markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 989-1002
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Sharp reliability bounds for the ℒ-like distributions, a class in which ageing is based on Laplace transform inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1204-1208
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
The closure of a local subexponential distribution class under convolution roots, with applications to the compound Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1194-1203
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
A renewal-process-type expression for the moments of inverse subordinators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1134-1144
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
A new urn model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 964-976
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Sensitivity of hidden Markov models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 632-642
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
On increasing-failure-rate random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 797-809
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Convergence results for compound Poisson distributions and applications to the standard Luria–Delbrück distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 620-631
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Asymptotic baseline of the hazard rate function of mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 892-901
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Minimum dynamic discrimination information models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 643-660
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
B-stability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-586
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Hidden regular variation and the rank transform
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 393-414
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
On the Nash equilibria for the FCFS queueing system with load-increasing service rate
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 461-481
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
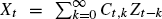 , generated by an array, {
, generated by an array, {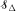 denote the class of local subexponential distributions and
denote the class of local subexponential distributions and 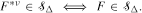 This result is applied to the infinitely divisible laws and some new results are established. The results obtained extend the corresponding findings of Asmussen, Foss, and Korshunov (2003).
This result is applied to the infinitely divisible laws and some new results are established. The results obtained extend the corresponding findings of Asmussen, Foss, and Korshunov (2003).