Refine listing
Actions for selected content:
524 results in 60Exx
Convolution Equivalence and Infinite Divisibility: Corrections and Corollaries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 295-305
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
First-crossing and ballot-type results for some nonstationary sequences
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 492-509
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Mean Residual Lifetimes of Consecutive-k-out-of-n Systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 82-98
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Arbitrary Threshold Widths for Monotone, Symmetric Properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 164-180
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Thou Shalt not Diversify: Why ‘Two Of Every Sort’?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 58-70
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On Generating Functions of Waiting Times and Numbers of Occurrences of Compound Patterns in a Sequence of Multistate Trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 71-81
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Comparison Results for Branching Processes in Random Environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 142-150
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Study of a Stochastic Failure Model in a Random Environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 151-163
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
General convex stochastic orderings and related martingale-type structures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 105-127
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Exact distributions for reward functions on semi-Markov and Markov additive processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1053-1065
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Normal characterization by zero correlations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 351-361
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Multivariate subexponential distributions and random sums of random vectors
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1028-1046
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Genealogy for supercritical branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1066-1076
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
A relation between positive dependence of signal and the variability of conditional expectation given signal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1181-1185
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Stochastic orders and majorization of mean order statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 704-712
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Asymptotics of the density of the supremum of a random walk with heavy-tailed increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 874-879
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
A discrete multivariate distribution resulting from the law of small numbers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 852-866
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
On stochastic recursive equations of sum and max type
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 687-703
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Hazard rate ordering of order statistics and systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-408
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Fractional Laplace motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 451-464
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
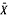 − μ)
− μ)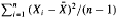 , and
, and 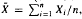 , then we show
, then we show 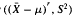 = 0 for
= 0 for 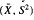 < 15/16, and this bound is the best possible.
< 15/16, and this bound is the best possible.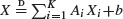 , and of max type,
, and of max type, 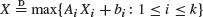 , where
, where 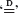 denotes equality in distribution. Equations of these types typically characterize limits in the probabilistic analysis of algorithms, in combinatorial optimization problems, and in many other problems having a recursive structure. We develop some new contraction properties of minimal
denotes equality in distribution. Equations of these types typically characterize limits in the probabilistic analysis of algorithms, in combinatorial optimization problems, and in many other problems having a recursive structure. We develop some new contraction properties of minimal 