Refine listing
Actions for selected content:
524 results in 60Exx
On customer flows in jackson queueing networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1094-1101
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Wiener-Hopf Factorization for a Family of Lévy Processes Related to Theta Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1023-1033
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
On zero-truncating and mixing Poisson distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1013-1027
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Discrete Scan Statistics Generated by Exchangeable Binary Trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1084-1092
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
SPECTRAL GAP FOR SOME INVARIANT LOG-CONCAVE PROBABILITY MEASURES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 22 November 2010, pp. 51-62
- Print publication:
- January 2011
-
- Article
- Export citation
Positive Dependence of Signals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 893-897
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
The Algebraic Degree of Phase-Type Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 611-629
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
On the number of runs for Bernoulli arrays
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 367-377
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Stochastic ordering of classical discrete distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 392-410
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Random effect bivariate survival models and stochastic comparisons
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-440
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Approximation for expectations of unbounded functions of dependent integer-valued random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 594-600
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
A class of location-independent variability orders, with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 407-425
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
THE SUBEXPONENTIAL PRODUCT CONVOLUTION OF TWO WEIBULL-TYPE DISTRIBUTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 18 May 2010, pp. 277-288
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Insensitive Bounds for the Moments of the Sojourn Times in M/GI Systems Under State-Dependent Processor Sharing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 246-267
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Generalized Increasing Convex and Directionally Convex Orders
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 264-276
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
On Occurrences of F-S Strings in Linearly and Circularly Ordered Binary Sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 157-178
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
The Joint Signature of Coherent Systems with Shared Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 235-253
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Generalized Measures of Divergence in Survival Analysis and Reliability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 216-234
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Optimal Allocation of Active Redundancies to k-out-of-n Systems with Heterogeneous Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 254-263
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Stein's Method for Compound Geometric Approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 146-156
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
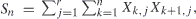 which denotes the number of consecutive pairs of successes (or runs of length 2) when reading the array down the columns and across the rows. With the case
which denotes the number of consecutive pairs of successes (or runs of length 2) when reading the array down the columns and across the rows. With the case 