Refine listing
Actions for selected content:
524 results in 60Exx
On the Joint Behavior of Types of Coupons in Generalized Coupon Collection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 429-451
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Increasing Hazard Rate of Mixtures for Natural Exponential Families
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 373-390
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
Pareto Lévy Measures and Multivariate Regular Variation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 117-138
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Continuous, Discrete, and Conditional Scan Statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 199-209
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
A Fourier Approach for the Level Crossings of Shot Noise Processes with Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 100-113
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Distribution of Clump Statistics for a Collection of Words
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1049-1059
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Some Inequalities of Linear Combinations of Independent Random Variables. I.
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1179-1188
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Convergence Properties in Certain Occupancy Problems Including the Karlin-Rouault Law
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1095-1113
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Exchangeability-type properties of asset prices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 666-687
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Signature-Based Representations for the Reliability of Systems with Heterogeneous Components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 856-867
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
On the Convolution of Heterogeneous Bernoulli Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 877-884
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Characterization of tails through hazard rate and convolution closure properties
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 123-132
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Exact Lower Bounds on the Exponential Moments of Truncated Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 547-560
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Improved Fréchet Bounds and Model-Free Pricing of Multi-Asset Options
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 389-403
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Processes with Block-Associated Increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 514-526
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Hazard Rate Properties of a General Counting Process Stopped at an Independent Random Time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 56-67
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
A Technique for Computing the PDFs and CDFs of Nonnegative Infinitely Divisible Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 217-237
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On the Skewness of Order Statistics in Multiple-Outlier Models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 271-284
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On Tails of Perpetuities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1191-1194
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Subexponential tails of discounted aggregate claims in a time-dependent renewal risk model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1126-1146
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
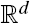 with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called
with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called 