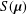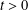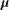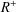Refine listing
Actions for selected content:
524 results in 60Exx
A Sharp Uniform Bound for the Distribution of Sums of Bernoulli Trials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 07 July 2015, pp. 352-361
-
- Article
- Export citation
The DFR Property for Counting Processes Stopped at an Independent Random Time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 574-585
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
EXACT UPPER AND LOWER BOUNDS ON THE DIFFERENCE BETWEEN THE ARITHMETIC AND GEOMETRIC MEANS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 149-158
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Stochastic Order Relations Among Parallel Systems from Weibull Distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 102-116
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Extreme Dispersions of Semicoherent and Mixed System Lifetimes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 117-128
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Permutation Monotone Functions of Random Vectors with Applications in Financial and Actuarial Risk Management
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 270-291
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
General inverse problems for regular variation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 229-248
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Finite-Dimensional Distributions of a Square-Root Diffusion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 930-942
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Two-node fluid network with a heavy-tailed random input: the strong stability case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 249-265
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Random Fields with Pólya Correlation Structure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1037-1050
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Uniform Chernoff and Dvoretzky-Kiefer-Wolfowitz-Type Inequalities for Markov Chains and Related Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1100-1113
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Nonnormal Small Jump Approximation of Infinitely Divisible Distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 963-984
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
STABLE AND SEMISTABLE PROBABILITY MEASURES ON CONVEX CONE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 20 November 2014, pp. 390-406
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Comparison Results for GARCH Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 685-698
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Asymptotic Bounds for the Distribution of the Sum of Dependent Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 780-798
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
A New Two-Urn Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 590-597
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
On the Joint Distribution of Stopping Times and Stopped Sums in Multistate Exchangeable Trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 483-491
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Dirichlet and Quasi-Bernoulli Laws for Perpetuities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 400-416
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Stochastic Orderings and Ageing Properties of Residual Life Lengths of Live Components in (n-k+1)-Out-Of-n Systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 58-68
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
On Exceedance Times for Some Processes with Dependent Increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 136-151
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation