We study certain stochastic processes arising in probabilistic modelling. We discuss the limit behavior of these processes and estimate the rate of convergence to the limit.

The concept of max-infinite divisibility is viewed as a positive dependence concept. It is shown that every max-infinitely divisible distribution function is a multivariate totally positive function of order 2 (MTP2). Inequalities are derived, with emphasis on exchangeable distributions. Applications and examples are given throughout the paper.

In this short note, we present a simple characterization of the increasing convex ordering on the set of probability distributions on ℝ. We show its usefulness by providing a very short proof of a comparison result for M/GI/1 queues due to Daley and Rolski, and obtained by completely different means.

The long-tailed Luria–Delbrück distribution arises in connection with the ‘random mutation’ hypothesis (whereas the ‘directed adaptation' hypothesis is thought to give a Poisson distribution). At time t the distribution depends on the parameter m = gNt/(a + g) where Nt is the current population size and g/(a + g) is the relative mutation rate (assumed constant). The paper identifies three models for the distribution in the existing literature and gives a fourth model. Ma et al. (1992) recently proved that there is a remarkably simple recursion relation for the Luria–Delbrück probabilities pn and found that asymptotically pn ≈ c/n 2; their numerical studies suggested that c = 1 when the parameter m is unity. Cairns et al. (1988) had previously argued and shown numerically that Pn = Σj ≧ n Pj ≈ m/n. Here we prove that n(n + 1)pn < m(1 + 11m/30) for n = 1, 2, ···, and hence prove that as n becomes large n(n + 1)pn , ≈ m; the result mPn ≈ m follows immediately.

There is a well-known connection between the asymptotic behaviour of the tail of the distribution of the increasing ladder height and the integrated tail of the step distribution of a random walk which either drifts to –∞, or oscillates and whose decreasing ladder height has finite mean. We establish a similar connection in a local sense; this means that in the lattice case we link the asymptotic behaviours of the mass function of the ladder height distribution and of the tail of the step distribution. We deduce the asymptotic behaviour of the mass function of the maximum of the walk, when this is finite, and also treat the non-lattice case.

Recently defined classes of life distributions are considered, and some relationships among them are proposed. The life distribution H of a device subject to shocks occurring randomly according to a Poisson process is also considered, and sufficient conditions for H to belong to these classes are discussed.

Consider a workstation with one server, performing jobs with a service time, Y, having distribution function, G(t). Assume that the station is unreliable, in that it occasionally breaks down. The station is instantaneously repaired, and the server restarts the uncompleted job from the beginning. Let T denote the time it takes to complete each job. If G(t) is exponential with parameter A, then because of the lack-of-memory property of the exponential, P (T > t) = Ḡ(t) =exp(−γt), irrespective of when and how the failures occur. This property also characterizes the exponential distribution.

We consider two weaker partial orderings among non-negative random variables. We derive some characterizations of the equivalence of two life distributions under the weaker orderings. These results lead to the characterizations of the equality of two non-negative random vectors in distributions by moments of extremes and sample mean. As the application of these results, we get various characterizations of the exponential distribution among HNBUE and HNWUE life distribution classes. The main results of Bhattacharjee and Sethuraman (1990), and Basu and Kirmani (1986) are special cases of these more general results.

Consider the total service time of a job on an unreliable server under preemptive-repeat-different and preemptive-resume service disciplines. With identical initial conditions, for both cases, we notice that the distributions of the total service time under these two disciplines coincide, when the original service time (without interruptions due to server failures) is exponential and independent of the server reliability. We show that this fact under varying server reliability is a characterization of the exponential distribution. Further we show, under the same initial conditions, that the coincidence of the mean values also leads to the same characterization.

An observer watches one of a set of Poisson streams. He may switch from one stream to another instantaneously. If an arrival occurs in a stream while the observer is watching another stream, he does not see the arrival. The experiment terminates when the observer sees an arrival. We derive a formula which states essentially that the expected total time that the observer watches a stream is equal to the probability that he sees the arrival in this stream divided by the intensity of the stream. This formula is valid independently of the observation policy. We also discuss applications of this formula.

Suppose that a device is subjected to shocks governed by a counting process N = {N(t), t ≧0}. The probability that the device survives beyond time t is then H̄(t)=Σk=0 ∞Q̄ℙ[N(t)=k], where Q̄k is the probability of surviving k shocks. It is known that H is NBU if the interarrivals Uk , ∊ ℕ+, are independent and NBU, and Q̄ k+j ≦ Q̄k · Q̄j holds whenever k, j ∊ ℕ. Similar results hold for the classes of the NBUE and HNBUE distributions. We show that some other ageing classes have similar properties.

This article investigates the accuracy of approximations for the distribution of ordered m-spacings for i.i.d. uniform observations in the interval (0, 1). Several Poisson approximations and a compound Poisson approximation are studied. The result of a simulation study is included to assess the accuracy of these approximations. A numerical procedure for evaluating the moments of the ordered m-spacings is developed and evaluated for the most accurate approximation.

Let A 1, A 2, …, An and B 1, B 2,. ., BN be two sequences of events on the same probability space. Let mn (A) and mN (B), respectively, be the number of those Aj and Bj which occur. Let Si,j denote the joint ith binomial moment of mn (A) and jth binomial moment of mN (B), 0 ≤ i ≤ n, 0 ≤ j ≤ N. For fixed non-negative integers a and b, we establish both lower and upper bounds on the distribution P(mn (A) = r, mN (B) = u) by linear combinations of Si,j , 0 ≤ i ≤ a, 0 ≤ j ≤ b. When both a and b are even, all mentioned S¡,j are utilized in both the upper and the lower bound. In a set of remarks the results are analyzed and their relation to the existing literature, including the univariate case, is discussed.

Lagrangian distributions are reviewed from the viewpoint of the Galton-Watson process. They are related to the busy period in queuing systems and to the first visit in random walks.

A property of the distributions is remarked for the application to vacant vehicles in a new transit system. Combinatorial identities of multinomial and binomial coefficients and related recurrences are shown by a probabilistic method. Based on the identities and recurrences, random forests generated by the Poisson and geometric Galton-Watson processes are characterized.

Stochastic majorization is a tool that has been used in many areas of probability and statistics (such as multivariate statistical analysis, queueing theory and reliability theory) in order to obtain useful bounds and inequalities. In this paper we study the relations among several notions of stochastic majorization and stochastic convexity and obtain sufficient (and sometimes necessary) conditions which imply some of these notions. Extensions and generalizations of several results in the literature are obtained. Some examples and applications regarding stochastic comparisons of order statistics are also presented in order to illustrate the results of the paper.

Shock models based on Poisson processes have been used to derive univariate and multivariate exponential distributions. But in many applications, Poisson processes are not realistic models of physical shock processes because they have independent increments; expanded models that allow for possibly dependent increments are of interest. In this paper, univariate and bivariate Pólya urn schemes are used to derive models of shock sources. The life distributions obtained from these models form a large parametric family that includes the exponential distribution. Even in the univariate case these life distributions have not been widely used, though they form a large and flexible family. In the bivariate case, the family includes the bivariate exponential distributions of Marshall and Olkin as a special case.

The first-order autoregressive semi-Mittag-Leffler (SMLAR(1)) process is introduced and its properties are studied. As an illustration, we discuss the special case of the first-order autoregressive Mittag-Leffler (MLAR(1)) process.

Let {Fn }n ≧ 0 be a sequence of c.d.f. and let {Rn }n ≧ 1 be the sequence of record values in a non-stationary record model where after the (n − 1)th record the population is distributed according to Fn. Then the equidistribution of the nth population and the record increment Rn – Rn – 1 (i.e. Rn – Rn – 1~ Fn ) characterizes Fn to have an exponentially decreasing hazard function. 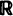To be more precise Fn is the exponential distribution if the support of Rn – 1 generates a dense subgroup in and otherwise the entity of all possible solutions can be obtained in the following way: let for simplicity the above additive subgroup be 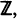any c.d.f. 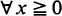F satisfying F(0) = 0, F(1) < 1 can be chosen arbitrarily. Setting λ = – log(1 – F(1)), Fn (x) = 1 – F(x – [x])exp(–λ [x]) is an admissible solution coinciding with F on the interval [0, 1] ([x] denotes the integer part of x). Simple additional assumptions ensuring that Fn is either exponential or geometric are given. Similar results for exponential or geometric tail distributions based on the independence of Rn – 1 and Rn – Rn – 1 are proved.

The paper investigates stochastic processes directed by a randomized time process. A new family of directing processes called Hougaard processes is introduced. Monotonicity properties preserved under subordination, and dependence among processes directed by a common randomized time are studied. Results for processes subordinated to Poisson and stable processes are presented. Potential applications to shock models and threshold models are also discussed. Only Markov processes are considered.

In this paper we introduce the concept of repair replacement. Repair replacement is a maintenance policy in which items are preventively maintained when a certain time has elapsed since their last repair. This differs from age replacement where a certain amount of time has elapsed since the last replacement. If the last repair was a complete repair, repair replacement is essentially the same as age replacement. It is in the case of minimal repair that these two policies differ. We make comparison between various types of policies in order to determine when and under which condition one type of policy is better than another.