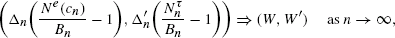Refine listing
Actions for selected content:
1047 results in 60Fxx
On maximum family size in branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 632-643
- Print publication:
- September 1999
-
- Article
- Export citation
Tightness of the stationary waiting time in heavy traffic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 788-794
- Print publication:
- September 1999
-
- Article
- Export citation
Uniform consistency of the partitioning estimate under ergodic conditions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-14
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
Central limit theorems for multivariate semi-Markov sequences and processes, with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 415-432
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotic behaviour for random walks in random environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 334-349
- Print publication:
- June 1999
-
- Article
- Export citation
Central limit theorem for a class of random measures associated with germ-grain models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 283-314
- Print publication:
- June 1999
-
- Article
- Export citation
On spectral gap estimates of a Markov chain via hitting times and coupling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 310-319
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotics of poisson approximation to random discrete distributions: an analytic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 448-491
- Print publication:
- June 1999
-
- Article
- Export citation
Weak convergence to the coalescent in neutral population models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 446-460
- Print publication:
- June 1999
-
- Article
- Export citation
Large deviations, moderate deviations, and queues with long-range dependent input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 254-278
- Print publication:
- March 1999
-
- Article
- Export citation
Large deviations in estimation of an Ornstein-Uhlenbeck model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 60-77
- Print publication:
- March 1999
-
- Article
- Export citation
The Frobenius–Harper technique in a general recurrence model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 30-47
- Print publication:
- March 1999
-
- Article
- Export citation
Existence and positivity of the limit in processes with a branching structure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 132-138
- Print publication:
- March 1999
-
- Article
- Export citation
Extreme values of phase-type and mixed random variables with parallel-processing examples
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 194-210
- Print publication:
- March 1999
-
- Article
- Export citation
Stationarity of a stochastic population flow model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 291-294
- Print publication:
- March 1999
-
- Article
- Export citation
Smallest-fit selection of random sizes under a sum constraint: weak convergence and moment comparisons
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 178-198
- Print publication:
- March 1999
-
- Article
- Export citation
Central limit theorem for wave-functionals of Gaussian processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 158-177
- Print publication:
- March 1999
-
- Article
- Export citation
Asymptotics of palm-stationary buffer content distributions in fluid flow queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 235-253
- Print publication:
- March 1999
-
- Article
- Export citation
Cell loss asymptotics for buffers fed with a large number of independent stationary sources
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 86-96
- Print publication:
- March 1999
-
- Article
- Export citation
Stably coalescent stochastic froths
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 199-219
- Print publication:
- March 1999
-
- Article
- Export citation
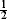 are small’, we show that there exists an invariant probability measure for ‘the environments seen from the position of (
are small’, we show that there exists an invariant probability measure for ‘the environments seen from the position of (