Refine listing
Actions for selected content:
1046 results in 60Fxx
A Central Limit Theorem for Contractive Stochastic Dynamical Systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 200-205
- Print publication:
- March 1998
-
- Article
- Export citation
Diffusion Approximation for Random Walks on Anisotropic Lattices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 206-212
- Print publication:
- March 1998
-
- Article
- Export citation
The return on investment from proportional portfolio strategies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 216-238
- Print publication:
- March 1998
-
- Article
- Export citation
Large Deviations for Queue Lengths at a Multi-Buffered Resource
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 240-245
- Print publication:
- March 1998
-
- Article
- Export citation
On the rate of growth of the overshoot and the maximum partial sum
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 181-196
- Print publication:
- March 1998
-
- Article
- Export citation
Non-Gaussian Density Processes Arising from Non-Poisson Systems of Independent Brownian Motions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 213-220
- Print publication:
- March 1998
-
- Article
- Export citation
Mechanical models for cell movement – locomotion, translocation, migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 827-846
- Print publication:
- December 1997
-
- Article
- Export citation
Stochastic fm models and non-linear time series analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 986-1003
- Print publication:
- December 1997
-
- Article
- Export citation
On the rate of convergence for extremes of mean square differentiable stationary normal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 908-923
- Print publication:
- December 1997
-
- Article
- Export citation
Stochastic Analysis of ‘Simultaneous Merge–Sort'
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 669-694
- Print publication:
- September 1997
-
- Article
- Export citation
Large deviations for departures from a shared buffer
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 753-766
- Print publication:
- September 1997
-
- Article
- Export citation
Corrected Diffusion Approximations for Ruin Probabilities in a Markov Random Walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 695-712
- Print publication:
- September 1997
-
- Article
- Export citation
Limit theorems for the total size of a spatial epidemic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 698-710
- Print publication:
- September 1997
-
- Article
- Export citation
Linear Programming Estimators and Bootstrapping for Heavy Tailed Phenomena
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 759-805
- Print publication:
- September 1997
-
- Article
- Export citation
Strong Approximations of Irreducible Closed Queueing Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 498-522
- Print publication:
- June 1997
-
- Article
- Export citation
On the second Borel-Cantelli lemma for strongly mixing sequences of events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 381-394
- Print publication:
- June 1997
-
- Article
- Export citation
Strong convergence of proportions in a multicolor Pólya urn
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 426-435
- Print publication:
- June 1997
-
- Article
- Export citation
Scanning Brownian Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 295-326
- Print publication:
- June 1997
-
- Article
- Export citation
Asymptotic Expansions in the Exponent: a Compound Poisson Approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 374-387
- Print publication:
- June 1997
-
- Article
- Export citation
The propagation of chaos of multitype mean field interacting particle systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 346-362
- Print publication:
- June 1997
-
- Article
- Export citation
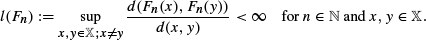
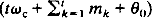 , where the message process {
, where the message process {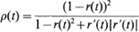
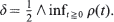 . We give bounds which are roughly of order
. We give bounds which are roughly of order 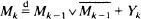 is investigated;
is investigated; 