Refine listing
Actions for selected content:
1046 results in 60Fxx
Probability metrics and recursive algorithms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 770-799
- Print publication:
- September 1995
-
- Article
- Export citation
Weak limit results for the extremes of a class of shot noise processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 707-726
- Print publication:
- September 1995
-
- Article
- Export citation
Ruin probabilities via local adjustment coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 736-755
- Print publication:
- September 1995
-
- Article
- Export citation
Large-deviation expressions for the distribution of first-passage coordinates
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 692-710
- Print publication:
- September 1995
-
- Article
- Export citation
A ratio limit theorem for (sub) Markov chains on {1,2, …} with bounded jumps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 652-691
- Print publication:
- September 1995
-
- Article
- Export citation
The probability of large queue lengths and waiting times in a heterogeneous multiserver queue I: Tight limits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 532-566
- Print publication:
- June 1995
-
- Article
- Export citation
The probability of large queue lengths and waiting times in a heterogeneous multiserver queue II: Positive recurrence and logarithmic limits
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 567-583
- Print publication:
- June 1995
-
- Article
- Export citation
A stochastic model for the movement of a white blood cell
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 443-475
- Print publication:
- June 1995
-
- Article
- Export citation
Limit theorems for stochastically perturbed dynamical systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 459-469
- Print publication:
- June 1995
-
- Article
- Export citation
A limit theorem for the replication time of a DNA molecule
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 296-303
- Print publication:
- June 1995
-
- Article
- Export citation
Runs on a circle
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 396-404
- Print publication:
- June 1995
-
- Article
- Export citation
Consistency of Hill's estimator for dependent data
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 139-167
- Print publication:
- March 1995
-
- Article
- Export citation
On the asymptotic size and duration of a class of epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 11-24
- Print publication:
- March 1995
-
- Article
- Export citation
On the local limit theorem for non-uniformly ergodic Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 52-62
- Print publication:
- March 1995
-
- Article
- Export citation
Statistics of the Boolean model: from the estimation of means to the estimation of distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 63-86
- Print publication:
- March 1995
-
- Article
- Export citation
An L 2 convergence theorem for random affine mappings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 183-192
- Print publication:
- March 1995
-
- Article
- Export citation
The convex hull of a normal sample
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 855-875
- Print publication:
- December 1994
-
- Article
- Export citation
Approximations of large trunk line systems under heavy traffic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1063-1094
- Print publication:
- December 1994
-
- Article
- Export citation
Poisson's equation for the recurrent M/G/1 queue
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1044-1062
- Print publication:
- December 1994
-
- Article
- Export citation
Dixie cups: sampling with replacement from a finite population
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 940-948
- Print publication:
- December 1994
-
- Article
- Export citation
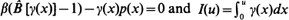 . It is shown that
. It is shown that 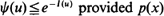 is non-decreasing and that log ψ(u) ≈ –
is non-decreasing and that log ψ(u) ≈ –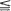
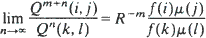
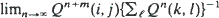 exists. An example shows that this limit may fail to exist if
exists. An example shows that this limit may fail to exist if 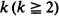 in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.
in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.