Refine listing
Actions for selected content:
1046 results in 60Fxx
The Gaussian distribution revisited
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 500-524
- Print publication:
- June 1996
-
- Article
- Export citation
On the asymptotic joint distribution of the sum and maximum of stationary normal random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 138-145
- Print publication:
- March 1996
-
- Article
- Export citation
Large deviations for discrete and continuous percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 29-52
- Print publication:
- March 1996
-
- Article
- Export citation
On improvements of the order of approximation in the Poisson limit theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 146-155
- Print publication:
- March 1996
-
- Article
- Export citation
Poisson and compound Poisson approximations for random sums of random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 127-137
- Print publication:
- March 1996
-
- Article
- Export citation
Large deviations and the Bayesian estimation of higher-order Markov transition functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 18-27
- Print publication:
- March 1996
-
- Article
- Export citation
Asymptotic distribution theory for Hoare's selection algorithm
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 252-269
- Print publication:
- March 1996
-
- Article
- Export citation
Conditional cyclic Markov random fields
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-12
- Print publication:
- March 1996
-
- Article
- Export citation
Multivariate normal approximations by Stein's method and size bias couplings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-17
- Print publication:
- March 1996
-
- Article
- Export citation
Bisexual branching diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 980-1018
- Print publication:
- December 1995
-
- Article
- Export citation
The extremal index and clustering of high values for derived stationary sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 972-981
- Print publication:
- December 1995
-
- Article
- Export citation
Compound Poisson approximations for word patterns under Markovian hypotheses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 877-892
- Print publication:
- December 1995
-
- Article
- Export citation
Some asymptotic results for exponential functionals of Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 930-940
- Print publication:
- December 1995
-
- Article
- Export citation
Limit theorems for the time of completion of Johnson-Mehl tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 889-910
- Print publication:
- December 1995
-
- Article
- Export citation
Large exceedences for uniformly recurrent Markov-additive processes and strong-mixing stationary processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 679-691
- Print publication:
- September 1995
-
- Article
- Export citation
A note on a model for restoring a destroyed region
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 756-767
- Print publication:
- September 1995
-
- Article
- Export citation
A central limit theorem for the isotropic random sphere
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 642-651
- Print publication:
- September 1995
-
- Article
- Export citation
Robustness of the Ewens sampling formula
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 609-622
- Print publication:
- September 1995
-
- Article
- Export citation
Limit theorems for the number of occurrences of consecutive k successes in n Markovian trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 727-735
- Print publication:
- September 1995
-
- Article
- Export citation
Random perturbations of recursive sequences with an application to an epidemic model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 559-578
- Print publication:
- September 1995
-
- Article
- Export citation
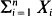 and
and 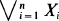 is derived under the condition
is derived under the condition  [0,∞). It is seen that the two statistics are asymptotically independent only if
[0,∞). It is seen that the two statistics are asymptotically independent only if 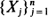 with state space consisting of the
with state space consisting of the 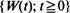 be a linear Brownian motion starting from 0. Following Dufresne (1989), (1990), De Schepper and Goovaerts (1992) and De Schepper et al. (1992), we are interested in the process
be a linear Brownian motion starting from 0. Following Dufresne (1989), (1990), De Schepper and Goovaerts (1992) and De Schepper et al. (1992), we are interested in the process 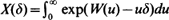 (for
(for 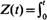 exp(
exp(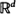 -valued random variables to a class of uniformly recurrent Markov-additive processes and stationary strong-mixing processes. As in the i.i.d. case, the results are proved via large deviations estimates.
-valued random variables to a class of uniformly recurrent Markov-additive processes and stationary strong-mixing processes. As in the i.i.d. case, the results are proved via large deviations estimates.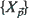 be a real-valued, homogeneous, and isotropic random field indexed in
be a real-valued, homogeneous, and isotropic random field indexed in 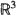 . When restricted to those indices
. When restricted to those indices 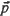 with
with 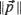 , the Euclidean length of
, the Euclidean length of 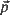 , equal to
, equal to 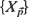 resides on the surface of a sphere of radius
resides on the surface of a sphere of radius 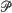 on the sphere, define
on the sphere, define 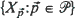 to be a realization of the random process and
to be a realization of the random process and 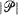 to be the cardinality of
to be the cardinality of 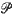 . Without specifying the dependence structure of
. Without specifying the dependence structure of 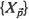 nor the marginal distribution of the
nor the marginal distribution of the 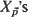 , conditions for asymptotic normality of the standardized sample mean,
, conditions for asymptotic normality of the standardized sample mean, 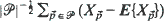 , are given. The conditions on
, are given. The conditions on 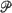 and
and 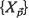 are motivated by the ideas and results for dependent stationary sequences.
are motivated by the ideas and results for dependent stationary sequences.