Refine listing
Actions for selected content:
1046 results in 60Fxx
Quasi-stationary distributions for a Brownian motion with drift and associated limit laws
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 911-920
- Print publication:
- December 1994
-
- Article
- Export citation
Estimating the home range
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 700-720
- Print publication:
- September 1994
-
- Article
- Export citation
Functional approximation theorems for controlled renewal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 765-776
- Print publication:
- September 1994
-
- Article
- Export citation
Strong Convergence of Stochastic Epidemics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 629-655
- Print publication:
- September 1994
-
- Article
- Export citation
A Functional Limit Theorem for the Total Cost of a Multitype Standard Epidemic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 690-697
- Print publication:
- September 1994
-
- Article
- Export citation
On a distributional bound arising in autoregressive model fitting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 401-408
- Print publication:
- June 1994
-
- Article
- Export citation
Generalized Bonferroni inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 409-417
- Print publication:
- June 1994
-
- Article
- Export citation
Rough limit results for level-crossing probabilities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 373-382
- Print publication:
- June 1994
-
- Article
- Export citation
Approximating gamma distributions by normalized negative binomial distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-400
- Print publication:
- June 1994
-
- Article
- Export citation
Archimedean copulas, exchangeability, and max-stability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 383-390
- Print publication:
- June 1994
-
- Article
- Export citation
A Central Limit Theorem for Cumulative Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 104-121
- Print publication:
- March 1994
-
- Article
- Export citation
A strong law and a central limit theorem for controlled Galton-Watson processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 22-37
- Print publication:
- March 1994
-
- Article
- Export citation
Convergence in Distribution of the One-Dimensional Kohonen Algorithms when the Stimuli are not Uniform
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 80-103
- Print publication:
- March 1994
-
- Article
- Export citation
Some joint distributions in Bernoulli excursions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 239-250
- Print publication:
- 1994
-
- Article
- Export citation
On large deviations of empirical measures in the τ-topology
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 41-47
- Print publication:
- 1994
-
- Article
- Export citation
Compound poisson approximations for the numbers of extreme spacings
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 847-874
- Print publication:
- December 1993
-
- Article
- Export citation
Limiting behaviour of two-level measure-branching
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 773-782
- Print publication:
- December 1993
-
- Article
- Export citation
Large deviations in the supercritical branching process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 757-772
- Print publication:
- December 1993
-
- Article
- Export citation
An asymptotically exact decomposition of coupled Brownian systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 819-834
- Print publication:
- December 1993
-
- Article
- Export citation
Extremal large deviations in controlled i.i.d. processes with applications to hypothesis testing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 875-894
- Print publication:
- December 1993
-
- Article
- Export citation
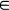 A
A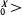 > t
> t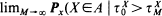 ) which is the law of a Bessel process with drift.
) which is the law of a Bessel process with drift.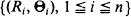 are the polar coordinates of the sightings, then is a sup-measure and corresponds to the right endpoint of the distribution
are the polar coordinates of the sightings, then is a sup-measure and corresponds to the right endpoint of the distribution 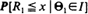 . The corresponding upper semi-continuous function
. The corresponding upper semi-continuous function 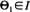 is in the domain of attraction of an extreme value distribution with bounded support, we are able to give an approximate confidence region.
is in the domain of attraction of an extreme value distribution with bounded support, we are able to give an approximate confidence region.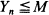 for
for 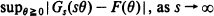 . In particular, we show that the exact order of uniform convergence is
. In particular, we show that the exact order of uniform convergence is 