Refine listing
Actions for selected content:
1046 results in 60Fxx
Sums and maxima of discrete stationary processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 863-876
- Print publication:
- December 1993
-
- Article
- Export citation
The probability that the largest observation is censored
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 602-615
- Print publication:
- September 1993
-
- Article
- Export citation
A Multilevel birth-death particle system and its continuous diffusion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 549-569
- Print publication:
- September 1993
-
- Article
- Export citation
Dynamics of an epidemic in a closed population
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 303-313
- Print publication:
- June 1993
-
- Article
- Export citation
Improved Poisson approximations for word patterns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 334-347
- Print publication:
- June 1993
-
- Article
- Export citation
Note on the strong limiting behaviour of busy periods in GI/G/1 queues under heavy traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 483-488
- Print publication:
- June 1993
-
- Article
- Export citation
Boundary-crossing probabilities of some random fields related to likelihood ratio tests for epidemic alternatives
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 52-65
- Print publication:
- March 1993
-
- Article
- Export citation
Asymptotic distribution of the maximum of n independent stochastic processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 66-81
- Print publication:
- March 1993
-
- Article
- Export citation
A martingale approach to the PASTA property
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 252-257
- Print publication:
- March 1993
-
- Article
- Export citation
Random splittings of an interval
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 131-152
- Print publication:
- March 1993
-
- Article
- Export citation
Joint exceedances of high levels under a local dependence condition
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 112-120
- Print publication:
- March 1993
-
- Article
- Export citation
Approximating kth-order two-state Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 861-868
- Print publication:
- December 1992
-
- Article
- Export citation
Asymptotic analysis of extremes from autoregressive negative binomial processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 904-920
- Print publication:
- December 1992
-
- Article
- Export citation
Simulating level-crossing probabilities by importance sampling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 858-874
- Print publication:
- December 1992
-
- Article
- Export citation
Limit theorems for the numbers of rare mutants: a branching process model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 778-794
- Print publication:
- December 1992
-
- Article
- Export citation
On the limiting distribution of a supercritical branching process in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 499-518
- Print publication:
- September 1992
-
- Article
- Export citation
On fast simulation of the time to saturation of slotted ALOHA
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 682-690
- Print publication:
- September 1992
-
- Article
- Export citation
Limit distributions for compounded sums of extreme order statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 557-574
- Print publication:
- September 1992
-
- Article
- Export citation
Limit theorems for suprema, threshold-stopped random variables and last exits of i.i.d. random variables with costs and discounting, with applications to optimal stopping
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 241-266
- Print publication:
- June 1992
-
- Article
- Export citation
A convergence theorem for symmetric functionals of random partitions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 280-290
- Print publication:
- June 1992
-
- Article
- Export citation
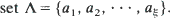 . We consider the number
. We consider the number 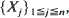 , and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of
, and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of 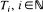
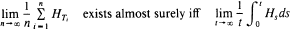
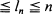 we find a necessary and sufficient condition on {
we find a necessary and sufficient condition on {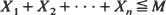 for every
for every 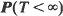 , by using Monte Carlo simulation and especially importance sampling techniques. When using importance sampling, precision and efficiency of the estimation depend crucially on the choice of the simulation distribution. For this choice we introduce a new criterion which is of the type of large deviations theory; consequently, the basic large deviations theory is the main mathematical tool of this paper. We allow a wide class of possible simulation distributions and, considering the case that
, by using Monte Carlo simulation and especially importance sampling techniques. When using importance sampling, precision and efficiency of the estimation depend crucially on the choice of the simulation distribution. For this choice we introduce a new criterion which is of the type of large deviations theory; consequently, the basic large deviations theory is the main mathematical tool of this paper. We allow a wide class of possible simulation distributions and, considering the case that 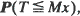 . The paper ends with an example.
. The paper ends with an example.