Refine listing
Actions for selected content:
1046 results in 60Fxx
Large deviations of heavy-tailed random sums with applications in insurance and finance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 293-308
- Print publication:
- June 1997
-
- Article
- Export citation
The product of independent random variables with slowly varying truncated moments
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 186-197
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
Compound Poisson limit theorems for Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 24-34
- Print publication:
- March 1997
-
- Article
- Export citation
Smoothing the Hill Estimator
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 271-293
- Print publication:
- March 1997
-
- Article
- Export citation
On a random vibration model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1141-1158
- Print publication:
- December 1996
-
- Article
- Export citation
Convergence of stochastic algorithms: from the Kushner–Clark theorem to the Lyapounov functional method
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1072-1094
- Print publication:
- December 1996
-
- Article
- Export citation
Functional limit theory for the spectral covariance estimator
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1077-1092
- Print publication:
- December 1996
-
- Article
- Export citation
Convergence rates for M/G/1 queues and ruin problems with heavy tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1181-1190
- Print publication:
- December 1996
-
- Article
- Export citation
The range of a simple random walk on ℤ
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1014-1033
- Print publication:
- December 1996
-
- Article
- Export citation
A central limit theorem for the parsimony length of trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1051-1071
- Print publication:
- December 1996
-
- Article
- Export citation
Rate of convergence of the fluid approximation for generalized Jackson networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 804-814
- Print publication:
- September 1996
-
- Article
- Export citation
Buffer overflow asymptotics for a buffer handling many traffic sources
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 886-903
- Print publication:
- September 1996
-
- Article
- Export citation
Heavy traffic analysis of a transportation network model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 870-885
- Print publication:
- September 1996
-
- Article
- Export citation
Economies of scale in queues with sources having power-law large deviation scalings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 840-857
- Print publication:
- September 1996
-
- Article
- Export citation
Asymptotic distributions for the Ehrenfest urn and related random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 340-356
- Print publication:
- September 1996
-
- Article
- Export citation
On heavy traffic approximations for transient characteristics of M/M/∞ queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 490-506
- Print publication:
- September 1996
-
- Article
- Export citation
Dynamic bandwidth allocation for ATM switches
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 758-771
- Print publication:
- September 1996
-
- Article
- Export citation
Large deviations in the piecewise linear approximation of Gaussian processes with stationary increments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 481-499
- Print publication:
- June 1996
-
- Article
- Export citation
Rates of convergence to normality for samples from a finite set of random variables
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 355-362
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
A point-process approach to almost-sure behaviour of record values and order statistics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 426-462
- Print publication:
- June 1996
-
- Article
- Export citation
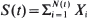 ,
, 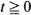 , where
, where 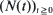 are non-negative integer-valued random variables and are
are non-negative integer-valued random variables and are 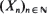 i.i.d. non-negative random variables with common distribution function
i.i.d. non-negative random variables with common distribution function 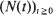 . Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function
. Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function 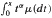 ) are investigated. Maller shows that if
) are investigated. Maller shows that if 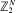 in continuous time
in continuous time 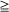 0 can be expressed in terms of binomial distributions; their limit behaviour for
0 can be expressed in terms of binomial distributions; their limit behaviour for 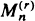 (the rth largest among a sample of
(the rth largest among a sample of 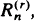 and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as
and differences and quotients involving them. In particular, we obtain characterizations of such asymptotic properties as 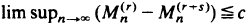 a.s. for some finite constant
a.s. for some finite constant 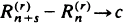 a.s. for some constant
a.s. for some constant 