Refine listing
Actions for selected content:
1046 results in 60Fxx
Asymptotic properties of the least-squares method for estimating transfer functions and disturbance spectra
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 412-440
- Print publication:
- June 1992
-
- Article
- Export citation
A central limit theorem by remainder term for renewal processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 267-287
- Print publication:
- June 1992
-
- Article
- Export citation
Limit laws for the maxima of chain-dependent sequences with positive extremal index
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 222-227
- Print publication:
- March 1992
-
- Article
- Export citation
Limit theorem and large deviation principle for the Voronoi tessellation generated by a Gibbs point process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 45-70
- Print publication:
- March 1992
-
- Article
- Export citation
On the existence of quasi-stationary distributions in denumerable R-transient Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 21-36
- Print publication:
- March 1992
-
- Article
- Export citation
Limit distributions of maximal segmental score among Markov-dependent partial sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 113-140
- Print publication:
- March 1992
-
- Article
- Export citation
The efficiency and heavy traffic properties of the score function method in sensitivity analysis of queueing models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 172-201
- Print publication:
- March 1992
-
- Article
- Export citation
Rates of strong convergence for U-statistics in finite populations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 468-480
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
Sampling Without Replacement: Approximation to the Probability Distribution
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-213
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
Limit theorems for triangular arrays under a relaxed asymptotic negligibility condition
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 117-128
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
On non-uniform and global descriptions of the rate of convergence of Asymptotic expansions in the central limit theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 326-335
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Poisson convergence for point processes on the plane
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-269
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
Remainder term estimates in a conditional central limit theorem for integer-valued random variables
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 75-85
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Stochastic compactness and point processes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-316
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
The theory of functional least squares
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 336-355
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
A central limit theorem for empirical processes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-248
- Print publication:
- October 1982
-
- Article
-
- You have access
- Export citation
On domains of partial attraction
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 328-331
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Limit theorems for samples from a finite population
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 318-327
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Some Properties of stochastic compactness
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 264-277
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
On the law of the iterated logarithm in the infinite variance case
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 5-14
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
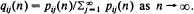 as
as 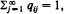 the distribution (
the distribution (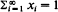 exists, where
exists, where 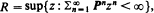 and T denotes transpose, then it is unique, positive elementwise, and
and T denotes transpose, then it is unique, positive elementwise, and 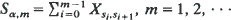 is determined by a realization
is determined by a realization 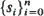 of states with s
of states with s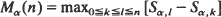 is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.
is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.