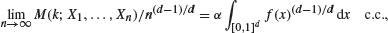Refine listing
Actions for selected content:
1046 results in 60Fxx
On the behaviour of a long cascade of linear reservoirs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 417-428
- Print publication:
- June 2000
-
- Article
- Export citation
Ergodic behaviour of extreme values
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 170-180
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
The growth of general population-size-dependent branching processes year by year
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-14
- Print publication:
- March 2000
-
- Article
- Export citation
Limit theorems for the minimal position in a branching random walk with independent logconcave displacements
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 159-176
- Print publication:
- March 2000
-
- Article
- Export citation
Compound Poisson approximation and the clustering of random points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 19-38
- Print publication:
- March 2000
-
- Article
- Export citation
Approximate entropy for testing randomness
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 88-100
- Print publication:
- March 2000
-
- Article
- Export citation
Probabilistic aspects of the SU(2)-harmonic oscillator
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 306-314
- Print publication:
- March 2000
-
- Article
- Export citation
Poisson limits for pairwise and area interaction point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 75-85
- Print publication:
- March 2000
-
- Article
- Export citation
Poisson limits and nonparametric estimation for pairwise interaction point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 252-260
- Print publication:
- March 2000
-
- Article
- Export citation
Asymptotic Behaviour of Continuous Time and State Branching Processes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 68-84
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
A central limit theorem for super-Brownian motion with super-Brownian immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1218-1224
- Print publication:
- December 1999
-
- Article
- Export citation
Asymptotic distribution of sum and maximum for Gaussian processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1031-1044
- Print publication:
- December 1999
-
- Article
- Export citation
The central limit theorem for Euclidean minimal spanning trees II
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 969-984
- Print publication:
- December 1999
-
- Article
- Export citation
Incomplete markets: convergence of options values under the minimal martingale measure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1058-1077
- Print publication:
- December 1999
-
- Article
- Export citation
Asymptotic properties of the connectivity number of random railways
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 720-741
- Print publication:
- September 1999
-
- Article
- Export citation
Asymptotics for geometric location problems over random samples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 632-642
- Print publication:
- September 1999
-
- Article
- Export citation
Weak approximations for empirical Lorenz curves and their Goldie inverses of stationary observations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 698-719
- Print publication:
- September 1999
-
- Article
- Export citation
Large deviations for the time of ruin
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 733-746
- Print publication:
- September 1999
-
- Article
- Export citation
A unified approach to fast teller queues and ATM
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 758-787
- Print publication:
- September 1999
-
- Article
- Export citation
On maximum family size in branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 632-643
- Print publication:
- September 1999
-
- Article
- Export citation
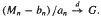 . In this paper, we shall show that {(
. In this paper, we shall show that {(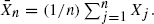 Under some mild regularity conditions on
Under some mild regularity conditions on 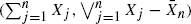 is obtained. Continuous-time results are also presented as well as a tube formula tail area approximation to the joint distribution of the sum and maximum.
is obtained. Continuous-time results are also presented as well as a tube formula tail area approximation to the joint distribution of the sum and maximum.