In this paper, we consider the stochastic sequence {Y t }t∊ℕ defined recursively by the linear relation Y t+1 = A t Y t + B t in a random environment which is described by the non-stationary process {(A t , B t )}t∊ℕ. We formulate sufficient conditions on the environment which ensure that the finite-dimensional distributions of {Y t }t∊ℕ converge weakly to the finite-dimensional distributions of a unique stationary process. If the driving sequence {(A t , B t )}t∊ℕ becomes stationary in the long run, then we can establish a global convergence result. This extends results of Brandt (1986) and Borovkov (1998) from the stationary to the non-stationary case.

We consider a stochastic model for the spread of an SIR (susceptible → infective → removed) epidemic among a closed, finite population that contains several types of individuals and is partitioned into households. The infection rate between two individuals depends on the types of the transmitting and receiving individuals and also on whether the infection is local (i.e., within a household) or global (i.e., between households). The exact distribution of the final outcome of the epidemic is outlined. A branching process approximation for the early stages of the epidemic is described and made fully rigorous, by considering a sequence of epidemics in which the number of households tends to infinity and using a coupling argument. This leads to a threshold theorem for the epidemic model. A central limit theorem for the final outcome of epidemics which take off is derived, by exploiting an embedding representation.

We consider a system where units having magnitudes arrive according to a nonhomogeneous Poisson process, remain there for a random period and then depart. Eventually, at any point in time only a portion of those units which have entered the system remain. Of interest are the finite time properties and limiting behaviors of the distribution of magnitudes among the units present in the system and among those which have departed from the system. We will derive limiting results for the empirical distribution of magnitudes among the active (departed) units. These results are also shown to extend to systems having stages or steps through which units must proceed. Examples are given to illustrate these results.

The multiplexing of variable bit rate traffic streams in a packet network gives rise to two types of queueing. On a small time-scale, the rates at which the sources send is more or less constant, but there is queueing due to simultaneous packet arrivals (packet-level effect). On a somewhat larger time-scale, queueing is the result of a relatively high number of sources sending at a rate that is higher than their average rate (burst-level effect). This paper explores these effects. In particular, we give asymptotics of the overflow probability in the combined packet/burst scale model. It is shown that there is a specific size of the buffer (i.e. the ‘critical buffer size’) below which packet-scale effects are dominant, and above which burst-scale effects essentially determine the performance—strikingly, there is a sharp demarcation: theso-called ‘phase transition’. The results are asymptotic in the number of sources n. We scale buffer space B and link rate C by n, to nb and nc, respectively; then we let n grow large. Applying large deviations theory we show that in this regime the overflow probability decays exponentially in the number of sources n. For small buffers the corresponding decay rate can be calculated explicitly, for large buffers we derive an asymptote (linear in b). The results for small and large buffers give rise to an approximation for the decay rate (with general b), as well as for the critical buffer size. A numerical example (multiplexing of voice streams) confirms the accuracy of these approximations.

A class of non-negative alternating regenerative processes is considered, where the process stays at zero random time (waiting period), then it jumps to a random positive level and hits zero after some random period (life period), depending on the evolution of the process. It is assumed that the waiting time and the lifetime belong to the domain of attraction of stable laws with parameters in the interval (½,1]. An integral representation for the distribution functions of the regenerative process is obtained, using the spent time distributions of the corresponding alternating renewal process. Given the asymptotic behaviour of the process in the regenerative cycle, different types of limiting distributions are proved, applying some new results for the corresponding renewal process and two limit theorems for the convergence in distribution.

Following Füredi and Komlós, we develop a graph theory method to study the high moments of large random matrices with independent entries. We apply this method to sparse N × N random matrices A N,p that have, on average, p non-zero elements per row. One of our results is related to the asymptotic behaviour of the spectral norm ∥A N,p ∥ in the limit 1 ≪ p ≪ N. We show that the value pc = log N is the critical one for lim ∥A N,p /√p∥ to be bounded or not. We discuss relations of this result with the Erdős–Rényi limit theorem and properties of large random graphs. In the proof, the principal issue is that the averaged vertex degree of plane rooted trees of k edges remains bounded even when k → ∞. This observation implies fairly precise estimates for the moments of A N,p . They lead to certain generalizations of the results by Sinai and Soshnikov on the universality of local spectral statistics at the border of the limiting spectra of large random matrices.

A generalisation of the classical general stochastic epidemic within a closed, homogeneously mixing population is considered, in which the infectious periods of infectives follow i.i.d. random variables having an arbitrary but specified distribution. The asymptotic behaviour of the total size distribution for the epidemic as the initial numbers of susceptibles and infectives tend to infinity is investigated by generalising the construction of Sellke and reducing the problem to a boundary crossing problem for sums of independent random variables.

This paper studies the geometric convergence rate of a discrete renewal sequence to its limit. A general convergence rate is first derived from the hazard rates of the renewal lifetimes. This result is used to extract a good convergence rate when the lifetimes are ordered in the sense of new better than used or increasing hazard rate. A bound for the best possible geometric convergence rate is derived for lifetimes having a finite support. Examples demonstrating the utility and sharpness of the results are presented. Several of the examples study convergence rates for Markov chains.

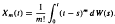Let {W(t), t ≥ 0} be a standard Brownian motion. For a positive integer m, define a Gaussian process Watanabe and Lachal gave some asymptotic properties of the process Xm(·), m ≥ 1. In this paper, we study the bounds of its moduli of continuity and large increments by establishing large deviation results.

The problem of discriminating between two Markov chains is considered. It is assumed that the common state space of the chains is finite and all the finite dimensional distributions are mutually absolutely continuous. The Bayes risk is expressed through large deviation probabilities for sums of random variables defined on an auxiliary Markov chain. The proofs are based on a large deviation theorem recently established by Z. Szewczak.

The paper considers one of the standard processes for modeling returns in finance, the stochastic volatility process with regularly varying innovations. The aim of the paper is to show how point process techniques can be used to derive the asymptotic behavior of the sample autocorrelation function of this process with heavy-tailed marginal distributions. Unlike other non-linear models used in finance, such as GARCH and bilinear models, sample autocorrelations of a stochastic volatility process have attractive asymptotic properties. Specifically, in the infinite variance case, the sample autocorrelation function converges to zero in probability at a rate that is faster the heavier the tails of the marginal distribution. This behavior is analogous to the asymptotic behavior of the sample autocorrelations of independent identically distributed random variables.

Haploid population models with non-overlapping generations and fixed population size N are considered. It is assumed that the family sizes ν1,…,νN within a generation are exchangeable random variables. Rates of convergence for the finite-dimensional distributions of a properly time-scaled ancestral coalescent process are established and expressed in terms of the transition probabilities of the ancestral process, i.e., in terms of the joint factorial moments of the offspring variables ν1,…,νN .

The Kingman coalescent appears in the limit as the population size N tends to infinity if and only if triple mergers are asymptotically negligible in comparison with binary mergers. In this case, a simple upper bound for the rate of convergence of the finite-dimensional distributions is derived. It depends (up to some constants) only on the three factorial moments E((ν1)2), E((ν1)3) and E((ν1)2(ν2)2), where (x)k := x(x-1)…(x-k+1). Examples are the Wright-Fisher model, where the rate of convergence is of order N -1, and the Moran model, with a convergence rate of order N -2.

A new representation for the characteristic function of the multivariate strictly geo-stable distribution is presented. The representation is appealing from a parametric viewpoint: its parameters have an intuitive probabilistic interpretation; and it is particularly useful for estimating the parameters of the geo-stable distribution.

A near-maximum is an observation which falls within a distance a of the maximum observation in an i.i.d. sample of size n. The asymptotic behaviour of the number K n (a) of near-maxima is known for the cases where the right extremity of the population distribution function is finite, and where it is infinite and the right hand tail is exponentially small, or fatter than exponential. This paper completes the picture for thin tails, i.e., tails which decay faster than exponential. Limit theorems are derived and used to find the large-sample behaviour of the sum of near-maxima.

It is common practice to approximate the cell loss probability (CLP) of cells entering a finite buffer by the overflow probability (OVFL) of a corresponding infinite buffer queue, since the CLP is typically harder to estimate. We obtain exact asymptotic results for CLP and OVFL for time-slotted queues where block arrivals in different time slots are i.i.d. and one cell is served per time slot. In this case the ratio of CLP to OVFL is asymptotically (1-ρ)/ρ, where ρ is the use or, equivalently, the mean arrival rate per time slot. Analogous asymptotic results are obtained for continuous time M/G/1 queues. In this case the ratio of CLP to OVFL is asymptotically 1-ρ.

We study the (two-sided) exit time and position of a random walk outside boundaries which are regularly varying functions of smaller order at infinity than the square root. A natural domain of interest is those random walks which are attracted without centring to a normal law, or are relatively stable. These are shown to have ‘stable’ exit positions, in that the overshoot of the curved boundary is of smaller order of magnitude (in probability) than the boundary, as the boundary expands. Surprisingly, this remains true regardless of the shape of the boundary. Furthermore, within the same natural domain of interest, norming of the exit position by, for example, the square root of the exit time (in the finite-variance case), produces limiting distributions which are computable from corresponding functionals of Brownian motion. We give a functional limit theorem for attraction of normed sums to general infinitely divisible random variables, as a means of making this, and more general, computations. These kinds of theorems have applications in sequential analysis, for example.

Suppose X 1,X 2 are independent random variables satisfying a second-order regular variation condition on the tail-sum and a balance condition on the tails. In this paper we give a description of the asymptotic behaviour as t → ∞ for P(X 1 + X 2 > t). The result is applied to the problem of risk diversification in portfolio analysis and to the estimation of the parameter in a MA(1) model.

Previous work on the joint asymptotic distribution of the sum and maxima of Gaussian processes is extended here. In particular, it is shown that for a stationary sequence of standard normal random variables with correlation function r, the condition r(n)ln n = o(1) as n → ∞ suffices to establish the asymptotic independence of the sum and maximum.

We consider a birth and growth model where points (‘seeds’) arrive on a line randomly in time and space and proceed to ‘cover’ the line by growing at a uniform rate in both directions until an opposing branch is met; points which arrive on covered parts of the line do not contribute to the process. Existing results concerning the number of seeds assume that points arrive according to a Poisson process, homogeneous on the line, but possibly inhomogeneous in time. We derive results under less stringent assumptions, namely that the arrival process be a stationary simple point process.

We formulate and verify an almost-sure lattice renewal theorem for branching random walks, whose non-lattice analogue is originally due to Nerman. We also identify the limit in these renewal theorems (both lattice and non-lattice) as the limit of Kingman's well-known martingale multiplied by a deterministic factor.