Refine listing
Actions for selected content:
1047 results in 60Fxx
On the role played by extreme summands when a sum of independent and identically distributed random vectors is asymptotically α-stable
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 437-454
- Print publication:
- June 2004
-
- Article
- Export citation
Convolution equivalence and infinite divisibility
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 407-424
- Print publication:
- June 2004
-
- Article
- Export citation
Large deviations for super-Brownian motion with immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 187-201
- Print publication:
- March 2004
-
- Article
- Export citation
Limiting distributions for minimum relative entropy calibration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 35-50
- Print publication:
- March 2004
-
- Article
- Export citation
The almost sure central limit theorem for one-dimensional nearest-neighbour random walks in a space-time random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 83-92
- Print publication:
- March 2004
-
- Article
- Export citation
Series representation and simulation of multifractional Lévy motions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 171-197
- Print publication:
- March 2004
-
- Article
- Export citation
Precise large deviations for sums of random variables with consistently varying tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 93-107
- Print publication:
- March 2004
-
- Article
- Export citation
A note on two-level superprocesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 202-210
- Print publication:
- March 2004
-
- Article
- Export citation
Some effects of trimming on the law of the iterated logarithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 253-271
- Print publication:
- 2004
-
- Article
- Export citation
The eigenvalues of the empirical transition matrix of a Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 347-360
- Print publication:
- 2004
-
- Article
- Export citation
Summability methods and negatively associated random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 231-238
- Print publication:
- 2004
-
- Article
- Export citation
On the foundations of multivariate heavy-tail analysis
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 191-212
- Print publication:
- 2004
-
- Article
- Export citation
Infinitely divisible approximations for discrete nonlattice variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 4 / December 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 982-1006
- Print publication:
- December 2003
-
- Article
- Export citation
Asymptotic geometry of high-density smooth-grained Boolean models in bounded domains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 4 / December 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 913-936
- Print publication:
- December 2003
-
- Article
- Export citation
Supercritical multitype branching processes: the ancestral types of typical individuals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 4 / December 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1090-1110
- Print publication:
- December 2003
-
- Article
- Export citation
Convergence to the coalescent with simultaneous multiple mergers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 839-854
- Print publication:
- September 2003
-
- Article
- Export citation
Transient behaviour of a Galton–Watson process with a large number of types
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1007-1030
- Print publication:
- September 2003
-
- Article
- Export citation
Random covering of the circle: the size of the connected components
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 563-582
- Print publication:
- September 2003
-
- Article
- Export citation
Ladder variables, internal structure of Galton–Watson trees and finite branching random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 671-689
- Print publication:
- September 2003
-
- Article
- Export citation
Large and small deviations of a string driven by a two-parameter Gaussian noise white in time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 4 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 946-960
- Print publication:
- September 2003
-
- Article
- Export citation
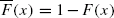 is consistently varying as
is consistently varying as 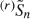 , which is obtained by deleting the
, which is obtained by deleting the 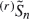 but not (completely) for
but not (completely) for 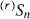 .
.