Refine listing
Actions for selected content:
1047 results in 60Fxx
Genealogy for supercritical branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1066-1076
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
The upcrossings index and the extremal index
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 927-937
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Some limiting properties of the bounds of the present value function of a life insurance portfolio
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1155-1164
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Asymptotics of the density of the supremum of a random walk with heavy-tailed increments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 874-879
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Large deviations for risk processes with reinsurance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-728
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Limiting crossing probabilities of random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 884-891
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Normal approximation for random sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 693-728
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
On the number of segregating sites for populations with large family sizes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 750-767
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
On the total length of the random minimal directed spanning tree
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 336-372
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
A central limit property under a modified Ehrenfest urn design
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 409-420
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
On a random-coefficient AR(1) process with heavy-tailed renewal switching coefficient and heavy-tailed noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 421-440
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Boundedly rational quasi-Bayesian learning in coordination games with imperfect monitoring
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 335-350
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Limit distribution of distances in biased random tries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 377-390
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Structured coalescent with nonconservative migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 351-362
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Central limit theorems for functionals of stationary germ-grain models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 76-94
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Diffusion Limit for Generalized Correlated Random Walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 60-73
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Large deviation probabilities for the number of vertices of random polytopes in the ball
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 47-58
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Markovian growth-collapse model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 221-243
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A Central Limit Theorem for Non-Overlapping Return Times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 32-47
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Rooted edges of a minimal directed spanning tree on random points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-30
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
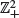 , with long-range weak dependence for each coordinate individually, usually present clustering of high values. For each one of the eight directions in
, with long-range weak dependence for each coordinate individually, usually present clustering of high values. For each one of the eight directions in 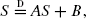 with specific independent random coefficients
with specific independent random coefficients 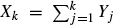 such that (
such that (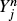 takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the
takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the 