Refine listing
Actions for selected content:
1047 results in 60Fxx
Limit theorems for stationary tessellations with random inner cell structures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 25-47
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Tools to Estimate the First Passage Time to a Convex Barrier
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 61-81
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
On the number of vertices with a given degree in a Galton-Watson tree
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 229-264
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Kalman-Bucy Filtering for Linear Systems Driven by the Cox Process with Shot Noise Intensity and Its Application to the Pricing of Reinsurance Contracts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 93-107
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
On the Effect of Finite Buffer Truncation in a Two-Node Jackson Network
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 199-222
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
The Large Deviations of Estimating Rate Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 267-274
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
A queue with semiperiodic traffic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 160-184
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Asymptotic Hitting Time for a Simple Evolutionary Model of Protein Folding
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 39-51
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Improving the performance of third-generation wireless communication systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1046-1084
- Print publication:
- December 2004
-
- Article
- Export citation
Occupation time processes of super-Brownian motion with cut-off branching
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 984-997
- Print publication:
- December 2004
-
- Article
- Export citation
Poisson approximation for (k 1, k 2)-events via the Stein-Chen method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1081-1092
- Print publication:
- December 2004
-
- Article
- Export citation
On pair and tuple formation under independent Poisson or renewal arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1138-1144
- Print publication:
- December 2004
-
- Article
- Export citation
Network decomposition in the many-sources regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 893-918
- Print publication:
- September 2004
-
- Article
- Export citation
Large deviations for supercritical multitype branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 703-720
- Print publication:
- September 2004
-
- Article
- Export citation
The log-normal approximation in financial and other computations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 747-773
- Print publication:
- September 2004
-
- Article
- Export citation
Random minimal directed spanning trees and Dickman-type distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 691-714
- Print publication:
- September 2004
-
- Article
- Export citation
Interacting reinforced-urn systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 791-804
- Print publication:
- September 2004
-
- Article
- Export citation
Limit theorem for continuous-time random walks with two time scales
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 455-466
- Print publication:
- June 2004
-
- Article
- Export citation
Limit theorems for iterated random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 425-436
- Print publication:
- June 2004
-
- Article
- Export citation
Convergence to the coalescent in populations of substantially varying size
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 2 / June 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 368-378
- Print publication:
- June 2004
-
- Article
- Export citation
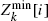 be the minimum possible population size at generation
be the minimum possible population size at generation 