Refine listing
Actions for selected content:
1047 results in 60Fxx
Extremes of regularly varying Lévy-driven mixed moving average processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 993-1014
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
On a localization property of wavelet coefficients for processes with stationary increments, and applications. I. Localization with respect to shift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 938-962
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
An epidemic model with exposure-dependent severities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 932-949
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
A large deviation principle for a Brownian immigration particle system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1120-1133
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
The closure of a local subexponential distribution class under convolution roots, with applications to the compound Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1194-1203
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Large-time asymptotics for the density of a branching Wiener process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1081-1094
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
A new urn model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 964-976
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
How to estimate the rate function of a cumulative process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1044-1052
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Power estimates for ruin probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 726-742
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Diffusion approximations for the maximum of a perturbed random walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 663-680
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Berry-Esseen bounds for combinatorial central limit theorems and pattern occurrences, using zero and size biasing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 661-683
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Convergence results for compound Poisson distributions and applications to the standard Luria–Delbrück distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 620-631
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Convergence results on multitype, multivariate branching random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 681-705
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
On asymptotically efficient simulation of large deviation probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 539-552
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
B-stability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 581-586
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Compound Poisson limits for household epidemics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 334-345
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Rarity and exponentiality: an extension of Keilson's theorem, with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 393-406
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Fluid limit of generalized Jackson queueing networks with stationary and ergodic arrivals and service times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 491-512
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Fragmentation energy
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 553-570
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
A Transposition Rule Analysis Based on a Particle Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 235-246
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
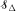 denote the class of local subexponential distributions and
denote the class of local subexponential distributions and 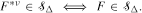 This result is applied to the infinitely divisible laws and some new results are established. The results obtained extend the corresponding findings of Asmussen, Foss, and Korshunov (2003).
This result is applied to the infinitely divisible laws and some new results are established. The results obtained extend the corresponding findings of Asmussen, Foss, and Korshunov (2003).