Refine listing
Actions for selected content:
1047 results in 60Fxx
Reduced Branching Processes with Very Heavy Tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 190-200
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Probabilistic Investigations on the Explosion of Solutions of the KAC Equation with Infinite Energy Initial Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 95-106
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Local properties of random mappings with exchangeable in-degrees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 183-205
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The Large Deviation Principle for the On-Off Weibull Sojourn Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 107-117
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Beat the Mean: Sequential Selection by Better Than Average Rules
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 244-259
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
The Pareto Copula, Aggregation of Risks, and the Emperor's Socks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 67-84
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON THE CLOSURE OF CONVOLUTION POWER MIXTURES (RANDOM SUMS) OF EXPONENTIAL DISTRIBUTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 1-7
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Precise Large Deviations for Sums of Random Variables with Consistently Varying Tails in Multi-Risk Models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 889-900
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
A Class of Infinite-Dimensional Diffusion Processes with Connection to Population Genetics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 938-949
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On a Theorem of Breiman and a Class of Random Difference Equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1031-1046
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
CLT-related large deviation bounds based on Stein's method
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 731-752
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Asymptotics for local maximal stack scores with general loop penalty function
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 776-798
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Asymptotic Behavior of a Generalized TCP Congestion Avoidance Algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 618-635
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
The Critical Galton-Watson Process Without Further Power Moments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 753-769
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Strong Convergence for URN Models with Reducible Replacement Policy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 652-660
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Asymptotic Expansions for Distributions of Compound Sums of Random Variables with Rapidly Varying Subexponential Distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 670-684
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Generalized Pólya urn Designs with Null Balance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 661-669
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Asymptotic Behavior of k-Word Matches Between two Uniformly Distributed Sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 788-805
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
A Lévy Process whose Jumps are Dragged by a Spherical Dynamical System
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 732-741
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Probabilistic Approximation of a Nonlinear Parabolic Equation Occurring in Rheology
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 528-546
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
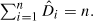 In the random digraph,
In the random digraph, 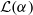 under convolution power mixtures (random summation).
under convolution power mixtures (random summation).